Quant: Time Value of Money

Question 1

How do we start a TVM problem?

Answer 1

Draw a TIMELINE

Question 2

Interest rates can be considered as…? (3)

Answer 2

Required rate of return (for compensation of risk) Discount rate (valuing future cash flows) Opportunity cost (of current consumption rather than saving)

Question 3

nominal risk free rate =

Answer 3

real risk free rate + exp inflation rate - real risk free rate assumes no exp inflation

Question 4

required interest rate on a security, r = [(5) factors]

Answer 4

real risk free interest rate + inflation premium + default risk premium + liquidity premium + maturity premium

Question 5

EAR (Effective Annual Rate) =

Answer 5

EAR = (1 + periodic rate)^m - 1 where: periodic rate = stated annual rate/m m = the number of compounding periods per year –> stated rate and EAR will only be equal when the stated rate compounds ANNUALLY (m=1)

Question 6

EAR (Convert annual stated rate to continuous compounding) =

Answer 6

= e^(annual stated rate) -1

Question 7

FV =

Answer 7

= PV (1+ r)^n For a regular/simple investment the PV is the single cash outflow (principle invested)

Question 8

FV (continuous compounding) =

Answer 8

= PV (e^[annual stated rate*n])

Question 9

PV =

Answer 9

= FV / (1+r)ⁿ

Question 10

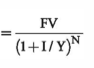
Difference between an annuity, ordinary annuity and an annuity due

Answer 10

An annuity is a stream of equal cashflows that occurs at equal intervals over a given period. Ordinary Annuity is characterized by cash flows that occur at the end of each compounding period. The other type of annuity is called an annuity due, where payments or receipts occur at the beginning of each period (i.e., the first payment is today at t=0).

(an annuity due essentially has an extra period of interest earned)

Question 11

Annuties: calculating FV & PV, Schw p106-108

For PV of an annuity, FV =

For an annuity where payment begins later than t =1:

Answer 11

For PV of an annuity, FV = 0

When payment begins after t =1, we have to do two steps (an ordinary annuity from the period before payment 1, and a regular discount back to t=0).

Question 12

Calculating FV of an annuity due =

Answer 12

a) use BGN mode on calculator

b)

Question 13

Calculating the PV of an annuity due =

Answer 13

a) use the beg mode in calculator
b) calculate PVAo (end mode) and multiply by the interest rate (to account for the extra interest earned)

PVAd = PVAo x (1+r), NB all else equal, the PV for an Ann Due is GREATER than PV for an Ord Ann

Question 14

PV of a perpetuity =

Answer 14

Note that the PV of a perp is the value one period before the next payment.

Question 15

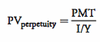
FV of a cash flow stream (uneven, therefore not an annuity) =

Answer 15

Calculate the FV of each individual cash flow, the first one will have the greatest N (number of periods of compouding), and sum together. MAINTAIN CORRECT SIGNS (+/-)

Question 16

PV of a (uneven) cash flow stream =

Answer 16

Sum the present value of each stream. N is larger for flows paid later.

OR use the NPV function on calculator

Question 17

Loan Payment Calculation (paying pack principle + interest on an amortizing loan) =

Answer 17

The unknown is PMT (N equal payments)

Enter I, PV (-), N and assume FV = 0 to find PMT

Adjust as necessary for payments that aren’t annual (N will increase - NxY, I will decrease I/Y)

Question 18

Breaking down interest and principal on a loan payment =

(NB. Need to clarify text on remaining principal)

Answer 18

Outstanding balance x I = interest portion

PMT - interest portion = principle portion

Question 19

CAG (compound annual growth rate) =

Answer 19

Use TVM function, enter PV, FV and N to find I (when given a number of annual figures). The starting figure will be PV, the final will be FV.

Question 20

Calculating payments to fund a future obligation (part 1)

Answer 20

Question 21

Calculating payments to fund a future obligation (part 2)

Answer 21

Question 22

Funding Future obligations: 2 Step (deposits made over period 1 to fund an annuity over period 2)

Answer 22

In calculating the amount required at year x for a 20 year annuity that will draw at the beginning of x, we can use TVM calculation with a) BGN, with N =20, or b) END, with N =19 and adding the PMT for year x in.

Question 23

Present Value =

Answer 23

How much would have to be deposited now in order to make particular withdrawals in the future, exhausting the account with the final withdrawal?

Question 24

Future Value =

Answer 24

How much would be in an account when the last of a particular series of deposits is made?

Question 25

Cash Flow Additivity Principle

Answer 25

Present value of any stream of cash flows = sum of the present values of the cash flows. The same is true for the future value of any stream of cash flows.

Question 26

Key Concept - LOS 5a

Answer 26

An interest rate can be interpreted as the rate of return required in equilibrium for a particular investment, the discount rate for calculating the present value of future cash flows, or as the opportunity cost of consuming now, rather than saving and investing.

Question 27

Key Concept LOS 5b

Answer 27

The real risk free rate is a theoretical rate on a single period loan when there is no expectation of inflation. Nominal risk free rate = real risk-free rate + expected inflation rate.

Securities may have several risks, and each increases the required rate of return. These include default risk, liquidity risk, and maturity risk.

The required rate of return on a security = real risk-free rate + expected inflation + default risk premium + liquidity premium + maturity risk premium.

Question 28

Key Concept LOS 5c

Answer 28

Question 29

Key Concept LOS 5d

Answer 29

For non annual time value of money problems, divide the stated annual interest rate by the number of compounding periods per year, m, and multiply the number of years by the number of compounding periods per year.

Question 30

Key Concept LOS 5e

Answer 30

Question 31

Key Concept LOS 5f

Answer 31

Constructing a time line showing future cash flows will help in solving many types of TVM problems. Cash flows occur at the end of the period depicted on the time line. The end of one period is the same as the beginning of the next period. For example, a cash flow at the beginning of Year 3 appears at time t = 2 on the time line.