Quant: Hypothesis Testing Flashcards
(25 cards)
What is a hypothesis?
A statement about the value of a population parameter developed for the purpose of testing a theory or belief.
Steps in Hypothesis Testing Procedure =
State the hypothesis
Choose appropriate test statistic
Specify the level of significance
State the decision rule regarding the hypothesis
Take a sample, calculate sample stats
Make a decision regarding the hypothesis
Make a decision based on the results of the test
Null hypothesis =
what we want to REJECT.
It is what is ACTUALLY tested, and is the BASIS for the test statistic chosen
always includes the “equal to” condition
Alternative hypothesis =
what we actually want to be TRUE (most of the time)
we conclude this if there is sufficient evidence to REJECT the null hypothesis
One tailed vs Two tailed tests =
one sided will be used to show that a value is greater than a single value.
a two tailed test will have 2 critical values/rejection points.
Test Statistic =
is a RANDOM VARIABLE that follows a T, Z, CHI-SQUARE or F distribution
calculated by comparing the point estimate of the population parameter and the hypothesized value of the parameter.
We then compare the TEST STATISTIC to the CRITICAL VALUE of the test statistic.

population
sample
sample statistic
WHAT IS THE CONNECTION?
we want to draw an inference regarding the parameter of a POPULATION. We take a SAMPLE of the population. We compute a SAMPLE STATISTIC. We draw our INFERENCE.
HOWEVER there is a chance that this SAMPLE is not representative of the popuilation–> ERROR!
when drawing inferences from a population -TYPE I ERROR =
rejection of the null hypothesis when it is actually true.
THE SIGNIFICANCE LEVEL is the chance of making a type 1 error - ie 5% significance level, means there is a 5% chance of rejecting the null when it should not be.
when drawing inferences from a population -TYPE II ERROR =
failure to reject the null hypothesis when it is actually false
chance of type II error INCREASES/power of test DECREASES with
- decrease in level of significance (ie from 5% to 1%)
- decrease in sample size
the POWER of the test =
1- P(making a TYPE II ERROR)
where a type II error is failing to reject the null when it is false.
We can use the power of the test to compare two different test statistics (and typically choose the one with THE GREATEST POWERS)
The power of the test increases whenyou reduce the chance of a type two error. This happens when you increase the significance level (ie. 1% to 5%), which increases the chance of making a type 1 error.
Seems we can take P.O.T as “the usefulness of the test in rejecting the null’
CHEAT CARD, T1 & 2 ERRORS, SIGNIFICANCE LEVELS AND POWER OF THE TEST=

Confidence interval =
A range of values within which the researcher believed the true population parameter may lie.
A 95% confidence interval uses a critical value associated with a particular distribution at a 5% level of significance.
A hypothesis test would compare a test statistic to a critical value at a 5% level of significance.
NB. standard error = s/√n
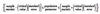
Statistical results vs economically meaningful results =
a statisitically significant result does not necessarrily mean an economically meaningful one: transactions costs, taxes and risk are not normally considered in the statistical test.
“Any of these factors could make committing funds to a strategy unattractive, even though the statistical evidence of positive returns is highly significant. By the nature of statistical tests, a very large sample size can result in highly (statistically) significant results that are quite small in absolute terms.”
P-value =
probability of obtaining a test statistic that would lead to the rejection of the null hypothesis when it is actually TRUE. Smallest level of significance for which the null hypothesis can be rejected.
take the test statistic, find the corresponding significance level from the distributiont (multiply by two if a two tailed test)
P- VALUE WILL SHOW THE LOWEST LEVEL OF SIGNIFICANCE FOR WHICH WE WOULD ACCEPT/REJECT THE NULL (THE THRESHOLD) - WHAT THE PROBABILITY IS THAT A VALUE WOULD BE GREATER THAN THE TEST STAT
t-test =
Use t-test when you could use a t distribution (DO YOU KNOW WHAT THE NECESSARY CONDITIONS ARE?)

z-test (variance known and unknown) =
Used when you could uses t stat (WHAT ARE THE CONDITIONS?)
The test compares a z-statistic with a critical z-value (which corresponds to the significance of the test)
If the variance is known, ‘σ’ becomes ‘s’, the sample standard deviation.

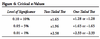
CHEAT CARD: CRITICAL Z-VALUES =
EXAMPLE FOR A T/Z TEST IS ON P316 OF SCHWESER
Hypothesis T-TEST: 2 populations, variance assumed to be EQUAL =
We are testing the hypothesis that the means of the two populations are equal.
Variances are unknown, but ASSUMED TO BE EQUAL.
Assumptions (‘we are reasonably certain that..”): populations are independent AND normally distributed.
SAMPLE OBSERVATIONS ARE POOLED.
KEY POINT: the numerator is the difference between sample means. The larger the difference, the bigger the t-stat, the more likely we are to reject the null and conclude the means are not equal (and vice versa if the numerator is small)

Hypothesis T-TEST: 2 populations, variance NOT assumed to be EQUAL =
We are testing the hypothesis that the means of the two populations are equal.
Variances are unknown, but NOT ASSUMED TO BE EQUAL.
Assumptions (‘we are reasonably certain that..”): populations are independent AND normally distributed.
BOTH SAMPLE VARIANCES ARE USED and T-TEST USES AN APPROXIMATED VALUE FOR THE DEGREES OF FREEDOM.
KEY POINT: the numerator is the difference between sample means. The larger the difference, the bigger the t-stat, the more likely we are to reject the null and conclude the means are not equal (and vice versa if the numerator is small)

Forming a hypothesis T-Test (2 populations, are the means equal) =
Hypothesis
Level of significance
T stat is calculated using craycray formulas
Deg of freedom is based on number of samples (n1+n2-2) if variance is assumed to be equal, calculated from craycray formula otherwise.
State the decision rule (what is the critical value and when we would reject the null)

Paired comparison test =
DATA MUST BE NORMALLY DISTRIBUTED
Used when samples may be dependent (ie returns of two steel companies, both would be affected by market returns and the same industry specific risks). We can’t use standard comparison T-TEST.
Test of whether the average difference between the observations of the two samples is SIGNIFICANTLY DIFFERENT FROM ZERO.
KEY POINT: t-test is with n-1 degrees of freedom, where n=number of paired observations.
t = avg diff in paired observations/std error of the differences between observations

Chi-square test =

for hypothesis tests for the variance of a normally distributed population.
ASSUMPTION: population is normally distributed.
Chi-square distribution is asymmetrical and approaches a normal distribution as DOF increase.

F-test =

for testing the equality of the variances of two populations.
ASSUMPTIONS: normally distributed and independent populations.
Can be two sided (Var1 = Var2) or one sided (Var1 > Var2)
For F-test always put the larger variance on top (numerator) - this lets us consider only the critical value in the right tail.

Parametric tests =
rely on assumptions about the distribution of the population and are specific to population parameters.
ie. Z-test: relies on mean and σ to define a normal distribution, requires population is normally distributed or sample is large.


