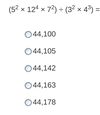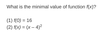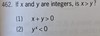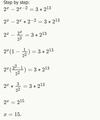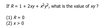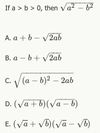Quant Strategy Flashcards

Question 1

Q

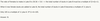
What do I want to remember when I see a DS formula problem?

Try problem

Answer

A

Always Simplify:

Question is really asking Does 2m = 3n?

Question 2

Q

How should you approach the first 30 seconds of every quant problem?

Answer

A

Close your eyes and take a deep breath, then assess:

Understand:

What type of problem is it (PS, DS)
What am I being asked for?
What am I given?
What can I jot down

Plan:

Have I seen something like this before?
What strategy do I want to apply?
Is there a formula, picture, table that would be helpul?

Solve:

Keep scratch paper systematic and organized
Bail (and guess) if you get stuck

Question 3

Q

How should you address the first 30 seconds of each Problem Solving question?

Answer

A

Scan the answer choices
- Type?
- Quality
- Symbols
- Spread
Is the problem Wordy / Math / Geometry?
Are there content clues?
- Key Words / Terms / Images
What strategies might work?
- Estimate / Make it real
- Smart #’s / Test Cases / Work Backwards?
- Content specific strategies (build a table, draw a picture)

Question 4

Q

How should you address the first 30 seconds of each Data Sufficiency question?

Answer

A

What is tangled?
- Question stem / statements / both?
Are the statements different or similar?
Is the problem Wordy / Math / Geometry?
Are there content clues?
- Key Words / Terms / Images
What strategies might work?
- Where do you need to rephrase (simplify first)?
- Which statement do you want to start with?

Question 5

Q

What should I make sure I remember when doing a decimal digits problem?

Try problem.

Answer

A

Make sure your remember to test cases?

Rounded decimals are dependent upon their following number.

Question 6

Q

What should I make sure I remember if I’m given two formulas, and asked for identify the value of two variables?

Answer

A

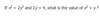
Use one formula to solve for the other!!

Question 7

Q

What should I make sure I remember if asked for distance between tickmarks on a linear scale?

Answer

A

Redraw the linear line
Find the LCM
Identify tickmark values
Identify distance

Question 8

Q

What do I want to remember when I see a Mixture problem?

Answer

A

If we’re given two variables that make up a total (e.g. X and Y totaling 300), we can solve for X by applying %’s and backing X out of Y.

The attached image is the algebra solution, but we can also work backwards!

Question 9

Q

What’s the first thing I want to remember when I see fractions, within fractions in a denominator?

Answer

A

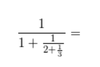
Simplify the denominator(s) by consolidating to term!
- e.g. if you have 2 + 1/3 in a demonitaor of a fraction, within another denominator of the fraction, you must first simplify 2+1/3 for 7/3s
- Then repeat this process for as may sub fraction denominators that you have

Question 10

Q

What do I want to remember when I see a problem with a factorial symbol “!”?

Answer

A

A factorial is the product of all the integers from 1 to to the factorial n. e.g. n! = (1)(2)(3)(4)…(n)

The sample problem is asking if k has a factor greater than one
- i.e. Is k a prime number or not?
If K is between 13! +2 and 13! + 13, then it is not prime, as (1)(2)(3)……(13) +2, and (1)(2)(3)….(13) + 13, as 2 would be a factor of 13! +2, and 13 would be a factor of 13! + 13.
- Both of these values are great than 1, which means K is not prime

Question 11

Q

Whats the first thing I want to identify when I see a probability question?

Answer

A

What is the probability asking for? How can I calculate it?

With the sample problem, your told that you have 100 balls #’ed 1-100
- The question asks whats the probabilty that the sum of 3 balls pulled will be odd?

What possible combinations give you and odd sum?
- Odd, Odd, Odd
- Odd, Even, Even,
- Even, Even, Odd
- Even, Odd, Even
If the balls are numbers 1-100, you have 50 opportunities to pull and odd number and 50 (50/100) = 1/2
1. Odd, Odd, Odd = (1/2)(1/2)(1/2) = 1/8
2. Odd, Even, Even, = (1/2)(1/2)(1/2) = 1/8
3. Even, Even, Odd = (1/2)(1/2)(1/2) = 1/8
4. Even, Odd, Even = (1/2)(1/2)(1/2) = 1/8
The sum of those 4 1/8ths = 4/8ths or 1/2

Question 12

Q

What is a Units Digit?

Answer

A

Units digit of a number is the digit in the one’s place of the number.

i.e It is the rightmost digit of the number.
For example, the units digit of 243 is 3, the units digit of 39 is 9.

Question 13

Q

What do I want to remember if a statement has variables squared?

Answer

A

Always consider negative #’s.

If the questions is asking for the value of something, and the statements include #’s squared, remember that even exponents hid the sign of the variable

Question 14

Q

What’s the the first thing I want to remember when asked for the missing length of the leg of a triangle?

Answer

A

The length of the longest side must be smaller than the sum of the lengths of the two other sides.

Question 15

Q

What’s the first thing I want to remember when calculating a probability with (an option removed a a coin removed)

Answer

A

The total probability will be the product of the two probabilities

Calculate the first probability
In this scenario because the coin is not replaced, it needs to be taken out of both the numerator and denominator in the second calc

Question 16

Q

What’s the first thing I want to remember when asked for the area of a trapezoid within a Triangle?

Answer

A

We can back into the area of the triangle, by calculating th encompassing (large triangle) as well as the remaining triangle (when considering whats left after looking at trapezoid)
If you see || this means the two lines are parallel
- Because they’re parallel you can calculate values for the other subsections using a ratio

Area of a Triangle = (1/2)bh
Area of a Trapedoid = h * Avg. of 2 bases (top / bottom)

Question 17

Q

What’s the first thing I want to remember when considering if question that lists an average within the statment?

Answer

A

Remember that the average will not immediately be negative if there are negative numbers in the data set. The average is the sum / the count.

Question 18

Q

Whats the first thing I want to remember when I see %’s in the answer choices?

Answer

A

Use Smart #’s to identify the answer

The answer options include half percents so let’s use 1,000 as a smart # base

Question 19

Q

Whats the first thing I want to remember when I see a # that is not large enough to be divisible by another number (e.g. 2 divided by 11)?

Answer

A

When a number is not large enough to be divisible by another number, it has a quotient of 0 with a remainder of whatever the number being dived is)

Question 20

Q

How do I want to set up an algebraic equation for the given word problem?

Answer

A

The ratio of 2 : 23 is given. We’re also told that there are 630 fewer buses than cars.

As such 2x + 630 = 23x

Question 21

Q

What do I want to remember when I see variables in the answer choices?

Answer

A

Use Smart #’s!

Pick a smart number
Calculate a value using your smart number
Plug your variable smart number into the answer options.
- The one that results in your hypotherical answer is the choice!

Question 22

Q

What do I want to remember when I see a right triangle?

Answer

A

Remember some right triangles have a ratio of 3 - 4 - 5
Can you back into the lengths of other legs with have these fractions?

Question 23

Q

What do I want to remember when informed that X is made up of the 2 digit positive integers a + b, and when I’m asked a question about X?

Answer

A

Remember that X is what the questions being asked about, not a + b.

The second statement says X + 7 is divisible by 9
- DON’T THINK YOU NEED TO CONSIDER Y, Y is not mentioned and X is already inclusive of the 2 variables a + b
With knowing X + 7 is divisible by 9, you can back into what the remainder of X / 9 would be

Question 24

Q

What’s the first thing I want to remember when I see this questions?

Answer

A

What is the question asking?
- Is X Prime
Statement 2 identifies that X has the same # of factors as Y² and that Y is a positive integer greater than 2
- If Y is greater than 2 and is squared, it at MINIMUM HAS A FACTOR OF ITSELF!!!
If Y² has more than 1 factor, and X has the same # of factors than X cannot be prime!!!!!

Question 25

Q

What do I want to consider when I see this question with variables in the question and fractions in the answers?

Answer

A

Use Smart #’s:

Don’t be fooled by the trickiness of the question
Is states If the committee selects y/x % of the black-and-white films
- This means that whatever you calculate y/x to be, you will then use that value as a %

Question 26

Q

What do I want to remember when I see exponents in a in a numerator and denominator?

Answer

A

You know you want to simplify
If the exponent is too large to simplify remember that you can always breakdown a number to its factors
- e.g. 12⁴ = (3⁴⁾(4⁴) you can now simplify

Question 27

Q

What do I want to remember when a DS questions asks for the remainder of a product divided by 2?

Answer

A

Remember that the greatest possible remainder for any number divided by 2 is 1

With that in mind, you can back into whether or not the variables included in the question are even or odd
With the even / odd identifications you can answer the question

This question is is an odds and evens question in disguise.

Question 28

Q

What do I want to remember when asked if a triangle is a right triangle?

Answer

A

Pythagorean Theorum states that in a right triangle a² + b² = c²

In order to determine if one a triangle is right, we would have to konw the value of all three sides, to see if in fact
- a² + b² = c²

Question 29

Q

What do I want to remember when plotting points / drawing a triangle on a coordinate plane?

Answer

A

When drawing on a coordinate plane, the distance between points, is between points, no from zero!

Question 30

Q

What’s the first thing I want to remember when I see fractions in the answer choices and %’s in this question?

Answer

A

Fractions and % tell me that I want to use SMART NUMBERS

The question tells you the % each person makes of the co-workers salary
Set the highest paid employee’s salary to 100, then identify other correlating salaries accordingly

Question 31

Q

What’s the first thing I want to remember when I get a coordinate plane question that asks for other points on the line?

Answer

A

Whats the slope of the line!

Rise over run (y/x)
Find the slope, and calculate the answer choices to see what has the same slope

Question 32

Q

What do I want to remember when asked for the value of a variable exponent like this?

Answer

A

We’re given then value of n, it = 10¹⁰ (i.e. 10 billion)

If n = 10¹⁰ then nⁿ = 10^{10 (with this exponent 10 being raised to the 10 10th’s as well)}
10 to the 10th power raised to 10 to the 10th power = 10^d
Eliminate bases and you have 10*10¹⁰ = d or 10¹¹ = d

Question 33

Q

What do I want to ensure I understand when I see a function of x (fx) question?

Answer

A

What is the question asking?

Question asks for the minimal value of the f(x)

In order to answer we need to know what the function of x is

Statement 1 tells us the value of (fx) for just on value of x. We have no idea about the other possible values
Statement 2 identifies the equation for the function. With the equation, we can calculate what the minimal value of x would be.

Question 34

Q

What do I want to remember when I see the below question?

If k is a positive integer, what is the remainder when (k+2)(k³-k) is divided by 6?

Answer

A

Remember that that questions says k is a positive integer.
- This means it could be any positive integer
Based on the answer choices we can use smart numbers to solve
It’s also possible that there’s no remainder, as shown in answer (A)
Whenever you see a variable to the third - that variable (e.g. (k³- k) remember that this simplifies to three consecutive integers k(k²-1) = k(k+1)(k-1)
- Rearrange to (k-1),k,(k+1)
- This represents three consecutive integers
Then not that you have (k+2) also in the equation, so you now have 4 consecutive integers to (k-1),k,(k+1),(k+2). Meaning we have the product of 4 consecutive integers 4!
- 4! = 24 (which is divisible by 6)
- So the product must be divisible by 6 as well

Question 35

Q

What do I want to remember when I see a consecutive integers question like this?

Answer

A

The question is showing a value for k in a range -26 < k < 24

Answer choices negative so this is probably testing something negative
If thats the range, draw out the first few numbers on each side of k
Notice that the number cancel out, except for the bookend of the negative range (-25 and -24) sum of those two is -49!!

Question 36

Q

What do I want to remember when addressing this problem?

Answer

A

Redraw the described image
You know that the angle opposite the length of the ladder must be 90^º
- If it’s 90 and the other angle is 60, the remaining angle must be 30 to total 180
- This is a specifal triangle 30: 60: 90 which has the following length ratio x : x√3 : 2x
With that ratio you can solve for the other leg lengths because you know the length of the hypotenuse 70

Question 37

Q

What’s the first thing I want to remember when looking at the answer choices in this Positives and Negatives questions?

Answer

A

Redraw the line
If a negative value of a number on a line is = to another value on the line, then those 2 #’s are equi-distance from 0
- Statement 1: q = -s
  - If S were 1 then -1 (s) = q. Both equal distance to 0
- If r is to the right of q and before s then it is closer to 0

Question 38

Q

What do I want to remember when seeing a Positives and Negatives problem like this?

Answer

A

Make sure when you’re working through this problem you copy the statements approrprately to your paper!
- 1) x + y > 0
- 2) y^x < 0
You have to test cases for both statements completely independent of each other, as in all DS questions

Question 39

Q

What do I want to remember when solving this exponent problem?

Answer

A

Simplify where I can.

Remember exponents with multiple variables are equal to the base raised to each variable individually
- e.g. 2^x-2 = 2^x* 2^-2
Once you have a like base you can factor out to solve

Question 40

Q

What do I want to remember when I see an algebraic translation question like this?

Answer

A

Remember Geometry formulas
- Area of a circle = πr²
- Diameter of a circle = 2r
- Circumference of a circle = πd or 2πr
- Area of a circle = s²
With the formulas in mind, you can back the amount of wire used for the circle out of 40, and identify the wire used for the square as the remainder

Question 41

Q

What do I want to remember when I see the options to this DS Algebraic translations question?

Answer

A

Looking at the answer choices if R = 0, then you know xy must = -1 (SUFFICIENT)
The second statement doesn’t give you anything. NOT SUFFICIENT

Question 42

Q

What do I want to recognize when I see an algebraic translation question like this?

Answer

A

The question is asking for the cost of milligrams, while the price has been giving in kg
Convert the kg price to mg and multiply by the quantity

$500/Kg and 600/mg in one pill.
1kg = 10⁶mg

(500/10⁶) * 600 = Cost per mg

Remember that you can convert the 500 to decimals, by counting the exponent #
- 10⁶ has 6 decimal places.
- 1. = 0.000500
0.0005 * 600 = .3

Remember when multiplying by decimals that you want to calculate the number of decimals in the both numbers and apply that to the final product

Question 43

Q

How would I solve a function question like this?

Answer

A

Don’t be scared of a function question. Understand it and figure out how to solve

The question is asking which of the functions listed in the answers would allow for the functions mentioned to work

Plug each of the functions into the two functions to see if they work

Question 44

Q

What do I want to remember when I see a ration problem like this?

Answer

A

What is the quesiton asking for?

How many ounces of concentrate are required to make 200 6 ounce cups of OJ?

What’s been given?

Ration of concentrate to water 1 : 3
Ounces in a can of concentrate 12
# of cups 200, number of ounces 6

How to solve

How many total ounces will we need? 200 * 6 = 1,200 ounces
Plug this into the ratio table you’ve made
- OJ = 1 : Water = 3 : Total = 4
- 1,200 is the total, which gives you a multipler of 300
- Apply the multipler to the OJ and water ratios
- OJ = 300 (1 * 300) and Water = 900 (3 * 300)
How many 12 ounce cans of concentrate go into a 300 ounces?
- 300/12 = 25

Question 45

Q

What do I want to remember when I see this problem?

Answer

A

Special Product 2: (a+b)(a-b) = a^2 - b^2

Question 46

Q

What do I want to ensure that I remember when I see an Arithmetic sequence question?

Answer

A

Understand: t_n=t_n−1−3 means that each term is 3 less than the previous term.
Plan if t₁= 23 and it’s asking for n when t_n = -4, then we’re solving for n when you’ve moved from 23 to -4
- 23 - (-4) = 27
- 27 / 3 = 9
So you’ve moved 9 spaces from t₁. 1 + 9 = 10
- So the correct answer is 10

Question 47

Q

What’s the first thing I want to remember when I see a Percentage growth problem?

Answer

A

A growth percentage won’t start from 0, unless explicitly stated

If you have a 20% growth after the first quarter, then you need to identify the basis, to calculate the growth between Q1 and Q2

Use 100 as your base to easily calculate

Question 48

Q

What do I want to remember when facing a percentage questions like this?

Answer

A

Read carefully!

Understand: Chance of selecting a student under 25
Plan:
- 48% M, 52% W; 40% M & 20% women > 25
- Use Smart numbers 100 Base
Solve:
- 48 M and 52 W
  - 1-40% = 60% M < 25
  - 1-20% = 80% W < 25
- 60% * 48 = 28.8 M < 25
- 80% * 52 = 41.6 W < 25
- 29 + 42 = 71 students under 25
- 71/100 = 70% answer B

Question 49

Q

What do I want to remembe when I’m given a ratio problem like this?

Answer

A

If you have multiple items being compared in the ratio:

Find the constant variable comparison
Build a multi-layer ratio table with all variables
- Normalize the constant and correlating ratios
This allows you to solve for the unknow multipler

Question 50

Q

What do I want to remember about variable values when presented with a DS question like this?

Answer

A

Remember that variables can be either positive or negative. You have to test cases to be sure

Statement 1:
- If the sum of x & y < 20, what are the possible values for x?
  - x = 25, y = -6 | X IS NOT UNDER 20
  - x = 19, y = 1 | X IS UNDER 20
- Due to the different answers NOT SUFFICIENT
Statement 2:
- Y is less than 20
  - y = 19, x = 1 | X IS UNDER 20
  - y =19, x = 5 | X IS NOT UNDER 20
- Due to the different answers NOT SUFFICIENT

Considering the 2 together

Y < 20
x and Y sum < 20
- x = 25, y = -6 | X IS NOT UNDER 20
- x = 19, y = 1 | X IS UNDER 20
Due to the different answers NOT SUFFICIENT

Question 51

Q

What’s the first thing I should think of when I see a percents problem like this one?

Answer

A

What’s 8% of 5,000?
- 400
Work backwards from the answers to identify which # has 400 as 6.5%
- Start with 5% of each answer to eliminate values that are too small
- Then you can calculate 1% and .5% respecively to identify the final answer

E must be right!

Question 52

Q

What do I want to remember when I see a DS question like this?

Answer

A

Whats being asked for: How many sweaters were sold?
- In order to identify number of sweaters sold I need to know total revenue and SP
Whats been given?
- From Question: Profit margin on Sweater
  - Need to calculate cost to identify selling price
- Statement 1: Total revenue $270
  - Ok this is 1 piece of the puzzle now I need SP
  - NOT SUFFICIENT
- Statement 2: Profit margin on sweater 50%
  - OK this is 1 piece of the puzzle, no I can back into selling price (1.5cost = 30; cost = $20)
  - Cost + profit: 20 + 30 = 50
  - NOT SUFFICIENT
- Together: Revenue $270, cost $50, now I can calculate the number of sweaters sold
  - SUFFICIENT

Question 53

Q

What do I want to remember when I see a problem like this?

Answer

A

The question includes variables, and lets you know that the value is between 0 and 1 (i.e. a fraction)

Because you have to calculate for a square root, pick a fraction that’s easy to take the root of (i.e. 1/4)

Question 54

Q

What do I want to remember when given an IR geometrical question like this?

Answer

A

What’s being asked?
- $ value to finish 2 spheres
What’s been given?
- Cost per square meter $92
- Formula for surface area of a sphere 4πr²
- Circumerference of spheres
  - 5.5M
  - 7.85
Plan
- You know the circumference formula = 2πr
- Use these to solve for r
  - 5.5 = 2πr
  - r = 5.5/2π
- Now that you have r you can plug this into the surface formula to calculate the cost
- Surface Area = 4πr²
- 4π(5.5/2π)²
  - Remember you can simplify down to 5.5²/π
  - Multiply this value by 92
Repeat the same for the other sphere

Question 55

Q

What do I want to remember when facing an IR question like this?

Answer

A

What’s the question asking for?
- value fo x and value for y that allows for a simple interest rate of 5
What’s been given?
- Simple interest formula r = 4x + 8y/x + y
- Original value of loans:
  - 10,000x at 4%
  - 10,000y at 8%
- Loan Z will consolidae the two
Plan
- What do I need to solve?
  - Ignore the 10,000 values as this is to confuse
- We simply need to plug 5 into the simple interest formulat and solve for x / y
Solve:
- 5 = (4x + 8y)/(x + y)
- This solves to x = 3y which is a ration for every 1 x there are 3 ys
- Which of the answer choices gives you that option?

Question 56

Q

What do I want to focus on when I see an IR question like this?

Answer

A

You have to make sure you understand what the graph is showing
- Horizontal axi shows Issue preference
- Vertical axis shows probability to vote
With this in mind the drop downs become easier to populate
The graph is identifying the probability that each person voted with their prior preference, not a change from AGAINST to FOR but rather the % that stayed with AGAINST or FOR.
1. e.g. Delta: 80% of those that had a preference of FOR voted FOR

Question 57

Q

What do I want to remember when I look at a DS question like this?

Answer

A

Trust your gut! You identified that there were overlapping data sets with conflicting averages. With that in mind it’s not possible to calculate an exact number.

Statement 1: Not sufficient, partial population
Statement 2: Not sufficient, partial population
Both statements together: Not sufficient, overlapping data sets with conflicting averages

Question 58

Q

What do I want to rememer when I see a PS Fractions (reciprocals) question like this?

Answer

A

Pay attention to what the question is asking for!
It says reciprocals so we know were dealing with a lot of really small fractions 1/43……….1/48
Theres no way we’ll find a LCD for these fractions, so we’ll have to estimate

Question 59

Q

What do I need to remember about exponents and signs in this problem?

Answer

A

Remember the following:

Negative exponents turn the base into a fraction
- e.g. 2^-2= 1/2² = 1/4
Negative odd exponents maintain the sign of the base
- -2^-1 = 1/-2¹ = 1/-2
- -3^-3 = 1/-3³ = 1/(-3 * -3 * -3) = 1/-27

Question 60

Q

How should I address this overlapping data sets question?

Question 61

Q

What do I want to remember when I see a DS question like this?

Answer

A

Set up a table to identify what’s been given, in the question, and whats been given in each statement to see if we can calculated what’s been asked for.

“Statements (1) and (2) Together are NOT sufficient

Question 62

Q

What do I want to remember when I see a question like this?

Answer

A

Remember that your formulas. Convert the problem to easy math

Question 63

Q

What do I want to remember when I see a fractions question like this?

Answer

A

Remember to solve for the unknown multipler and read the answer choices!

Question 64

Q

What do I want to remember about Standard Deviation?

Answer

A

The standard deviation will not change if each variable is changed by the same amount

Answer 64

A

If a triangle is on a coordinate plane, and the lines aren’t horizontal / vertical, calculate the area of the surrouding rectangle / triangles to find it’s area.

Answer 65

A

You know time is constant as both drivers are in the same car

Back into the ration of time Tom spent driving (3/5)
To get the ratio of Peter to Tom Divide Peters rate by toms
- 2/5 divided by 3/5 gives you 2/3 or 2:3 the ration

Answer 66

A

What’s constant? The base fee

Back the base fee out of the total and solve for the remainder

Answer 67

A

Although you can identify the numbers who’s products total 14, remember that these number could be in any order 127, 217, 712, etc.

Because you can’t identify one consistent answer, neither statement is sufficient

Answer 68

A

This is a variable question in which you’re given the variables in two separate equations:

Use each equation to solve for the value of 1 variable, and then plug that into the the other formula

Answer 69

A

TEST CASES!

Testing cases will easily identify the right answer

Answer 70

A

Don’t eliminate choices too early.

Remember idiom Not only, but also
If the “Not only” isn’t included, “but it also” would work

Answer 71

A

Find which Fractions have the same denominator and eliminate easy wrong answers
Identify how to compare the remaining?
- Easier to simplify some of the larger fractions to make them comparable
- If you have simplified fractions with at least one common denominator, you can normalize by multiplying by the the common variable over 1

Correct answer is D

This is Quantitative :: Problem Solving:: 11561 from the GMAT problem set.

Answer 72

A

Remember the limitations
- You are selecting 3 people from a group of 10
- The 10 candidates are made up of 5 couples and you cannot select two people that are married
Option 1: Can be any of the 10 people
Option 2: Cannot be the option 1 selection, or Option 2 selection, so 8 available option (10-2)
Option 3: Cannot be option 1 or 2 selections, or their respective spouses, so 6 available options (10-4)
- You have 6 potential ordering for those 3 people

(10 * 8 * 6) / 6 = 80

You can also think about it differently using the combination calculation approach:

We have 5 couples, from which we need to select 3 people
We can the select one person from each couple selected
Stage one, how many combinations of folks from the three couple selection?
- 5C3 = 10
  - This approach: https://www.youtube.com/watch?v=05a0A7vjG8I&t=248s)
- The first 3 factors in 5! divided by 3! = (5 * 4 * 3) / (3 * 2 * 1).
  - This is a simplified version of n! / r!(n-r)!
We then have to select 1 from each couple
- We have the option of selecting each person so thats 2 options from each couple 2 * 2 * 2 = 8
10 * 8 = 80

Answer 73

A

Remember to read carefully and test cases
Although you’re given rate of one machine and are told that 1 machine operates at twice the rate of the other, we’re not told which machine we’ve been given the rate for.
- Calculation output could be different dependent upon the question

Answer 74

A

Identify what’s been provided
- N is even
- When N is / 9 there’s a remainder of 8
What’s being asked?
- Which of the values (1, 4, 9, 10, 17) if added to N would maek it divisible by 18 (which is a multiple of 9)

Need to think of this like algebraic translation:

N = 9(multiplied by sum #) + 8 (because there’s a remainder of 8 when N is divided by 9)
- n = 9q + 8
Now we can plug the answer choice in to see how it effects our formula

Answer 75

A

What’s being asked?
- How many bottles of C were ordered?
What’s been given?
- Total bottles 63

In order to solve we need to identify the ratio of the bottles ordered

Statement 1: R = .8 of G
- This does not provide us with a ratio to the total or to C
- NS
Statement 2: C = .75 of (R+G)
- We now how C relates to the other two drinks
- All we need to do now is identify how the two drinks relate to 63
- We can back into this answer!
- Sufficient

Answer 76

A

Remember that each team is playing each team once (so games can’t be double counted as unique, between each team)
- e.g. when team A plays team B, that is a unique game on both team A and team B’s schedules, so A vs. B, is the same as B vs. A
Map out a the first few games on a few of the teams schedules
- You’ll see that theres a decreasing number of unique games
You can either estimate an answer or use the sum of consecutive integers formula (Avg.) * # of terms
1. To use this formula you must remember the start and end of the unique game values
Easiest way is to use the Combinations Formula: n!/(r!(n-r)!)

Answer 77

A

Similar to a race problem, if the order in which things take place matters, then it changes our formula
- In a race, if runner A finishes first, runner B, second, and runner C third, this is 1 unique list
  - If runner B finishes first and A finished second and C finishes third, this is a seperate unique list
  - Although the same participants, their orders are different and the order matters
The Combinations formula changes from: n!/(r!(n-r)!) to
- n!/(n-r)!

Answer 78

A

Although this is a combinatorics problem, you may not be able to use the combinatorics formula
Use the Slot method

How to solve:

Digit 1 can be 8 possible values (anything other than 0,1)
Digit 2 can be 1 digit, with two possible values (that will have two different effects)
- If Digit 2 is 0, then Digit 3 will have (9 possible values 1-9)
- If Digit 2 is 1, then Digist 3 will have 10 possible values 0-9)
Calculate the possibilities and add them together:
- Possibility 1: 8 * 1 * 9 = 72
- Possibility 2: 8 * 1 * 10 = 80
  - Sum = 152

Answer 79

A

You’ve been given the range
- Range is the dial which has 8 intervals
- You’ve been given values for some of the intervals
The ask: Where will the pointer stop after 1,174 intervals?

Don’t think about dividing the 1174 by the interval values, as this will give you potentially multiple values.

First identify how far each lettered interval is
- 1 = Blank, 2 = A, 3 = B, 4 = C, 5 = D, 6 = E, 7 = Blank, 8 = S
Now remember that the dial has 8 intervals in total
- Can 8 divide equally into 1,174?
  - No it cannot. You’ll arrive at ~146 and some change
- Now we know what the closest multiple of 8 to 1,174
Multiple 8 by 146 = 1,168
1,174 - 1,168 = 6.
Because the pointer is at S after 1,168 intervals, it will have to travel 6 more intervals to land at 1,174.
Which letter has an interval of 6?
E

Answer 80

A

Because of the variables in question this requires calculating both the combined and alternative probabilities:

Remember what’s been given, what’s been asked and how to get there

Given: Apples and Oranges in each basket
Ask: Probability of 1 apple and 1 oranges being selected
How to get there?
- We need to calculate both probabilitites separately and add them together

Combined Probability 1: You select an apple from box 1 and an orange from box 2

A = 4/6 of box 1, Oranges = 5/8 of Box 2
- Multiply the two to get a probability of 20/48

Combined Probability 2: You select 1 orange from box 1 and one apple from box 2

A = 3/8, O = 2/6
- Multiply the two to get a probability of 6/48

Alternative probabilities: Add the two probabilities together to get your total alternative probability 20/48 + 6/48 = 26/48 = 13/24

Answer 81

A

When solving for probabilities you want to initially identify what the probability is asking for?

Probability of Alternatives: e.g. Selecting 1 apple and 1 orange, or selection from a deck of cards bein divisible by 2 or divisible by 7
Combined Alternatives: e.g. Neither pen selected from a box will be defective.

When solving for alternatives you are calculating the probabilities separately, and then adding those probabilities together
When solving for combined alternatives you are calculating the probabilities separatelh then multiplying them by eachother

Answer 82

A

Be mindful of what the question is asking for and what’s been given

What’s being asked? Least possible value of the actual area
What’s been given? Side length, rounded to the nearest centimeter is 6 centimiters

Because the question states that 6 is rounded to the nearest centimeter than the possible side values are 5.5 ≤ x < 6.5

Now calculate the area of a square region with a length of 5.5
- 5.5² = 30.25

Answer 83

A

What’s been given?
- The window is made up of a rectangle and a semi-circle
  - not a complete circle. Keep this in mind when calculating area
What’s being asked: What’s the area of the window

Area of the semi circle
- Are of a circle = πr²
  - D given = 4
  - r = d(1/2)
  - Area of circle = π2² = πr4
  - Area of the semi-circle = 1/2(π4) = π2
Area of a rectangle
- Base * Height
  - Base = 4
  - Height = 10 - (radius of semi circle 2) = 8
  - 4 * 8 = 32
Total area = 32 + π2

Answer E

Answer 84

A

What’s being asked?
- Asking for the which of the answers equals the height of the carton
What’s been given?
- Length, width, height ration 3:2:2
How would I solve?
- Let’s use smart numbers
- Draw the carton with the metrics L = 3, W = 2, H = 2
- Calculate the volume of the carton as 3 * 2 * 2 = 12

Now plug the volume X (12) into the formulas in the answer choices to see which one equals 12

Answer B works

Answer 85

A

What’s being asked: Is the result of a formula divisible by 15?
Whats been given?
- Formula x¹⁶- y⁸ + 345y²
- Statements

Solving: When looking at the equation realize that 345 is divisible by 15, as such, we no longer need to consider it as a part of the problem.

Now our modified ask is is x¹⁶- y⁸ divisibile by 15

Answer 86

A

If you have two consecutive even integers, one of them is always divisible by 4, and the product of those two would be divisible by 8 (2 * 4)
How many times would a consective group of integers be divisible by 8?
- How would we determine this?

Answer 87

A

What is the question asking for?
- Probability that 3 balls selected, 1 will be green, and the 2 others will not be yellow
What’s been given?
- 10 balls: 1 green, 1 yellow?
How to solve?
- There are three alternatives here because there are three separate ball selections, but we have to calculate the scenarios for each (combined probabilities) then sum them to identify the alternative probability

Answer 88

A

What’s been asked?
- Probability that in choosing 4 individuals socks, that 2 are the same color?
What’s been given?
- Your population has three separate colors (White, Black, Grey)
- Number of pairs of each color of sock
How can I solve?
- Realize that you’re picking 4 individual socks, from a population including three different colors
- Regardless of the # of paired of each color of socks, there is a 100% change you will pick 2 of the same color, because their are less variants than you are picking

Answer 89

A

You have to assess the information given prior to being able to solve:

Statement 1 tells you that y is < = 8
Statement 2 tells you that y is >= 4

You have to understand how each of these numbers effects the probability before you can answer.

Answer 90

A

Identifying that this question requires the prime identification of the product number, to find the answer:

The question identifies that this is a prime multiplication question by saying “if the product of the point values of the selected chips is 88,000, how many purple chips were selected)

Answer 91

A

Identify that the existing ratio is given 30:36 or 5:6
- Total of 11: 5+6 =11
Then you’re adding 6 females to the ratio
As such, the answer can only be a multiple of 11 + 6

Test the answer choices to see which one fits.

Answer 92

A

W = R * T

You’re given the information required to calculate each persons rate
- A = 50 per hour
- B = 55 per hour
  - Collectively 105 / hour (50 +55)
Plug this into the formulat to identify how long it will take the two working together
1,400 = 105 * T
T = 1,400 / 105

Beware not to convert the rate to minutes too early.

Answer 93

A

Remember that an average hides the actual # of days taken by employee, and that it could be drastically effected by outliers. With that in mind, applying %’s to an average, would have varying outcomes, without knowing the specific employees vacation days.

Answer 94

A

Always map out a coordinate plane question
Slope formula y = mx + b
- If the x intercept is given, then we can solve the equation as follows
- x =6
- Y will always be zero at the x-intercept
- Line formula provided y = 2x + b
- 0 = 2(6) + b
- b = -12

By drawing the plane, you’ll see that the y intercept must be negative

Answer 95

A

For any product to be even, only one of the variables has to be even
Product will also be odd if all variabls are odd

To solve we must determine if x,y,p are odd or even

Answer 96

A

Look at the answer choices, I could have worked backwards to identify the correct answer
Or solve algebraically
- If solving algebraically and you have two factors that make up a whole, remember how to set up the equation
- Let x = 20 ounce bottles, let 48-x represent the 40 ounce bottles
- (x(20) + (48-x)(40))/48 = 35

Answer 97

A

Identify how to solve
TEST CASES!!!!

Answer 98

A

Identify how to solve
TEST CASES!!!

Answer 99

A

Understand how the formula works
- P = -2(S-4)² + 32
  - In looking at this because the parenthese are multiplied by -2, that product will always be negative, unless the parentheses sum was 0
  - Which answer will give us zero?

Answer 100

A

A Triangle within a semi-circle is always a right triangle
30: 60 :90 triangles has a length ratio of 1: √3 : 2

Answer 101

A

Don’t rush!
Pay attention to the sign!!!

Answer 102

A

Don’t rush
Pay attention to the sign!
When the question is asking about which formula doesn’t have a root in common, it means which formula doesn’t simplify down to one of the potential values of the formula in question

Answer 103

A

Parallelograms are made up of:
- Squares: All sides are equal and all angels are 90°
- Rectangeles: All angels are 90° and diagonals are equal
- Rhomubuses: All sides are equal

Answer 104

A

Permutation calculation when order matter:
- Order matters, more variations possible (no extra r)
Combination when order doesn’t matter
- Order doesn’t matter, fewer possibilities (extra r)

Answer 105

A

Remember that the complete quadratic equation must be equal to 0 in order to identify the possible values of x
When the GMAT provides the square root sign for an even root, such as a square root, fourth root, etc. then the only accepted answer is the positive root.

Answer 106

A

As the problem asks for the smallest number, and all of the fractions are over 1, the number with the biggest denominator will be the smallest number
To solve more rapidly, recognize that all of the denominators include 5 raised to some power
- You can normlize the 5^s to make it easier to identify the biggest denomintor
- Remember that if you’re multiplyng the 5^ in the denominator, to increase the exponent, then you have to divide the other factor in the denominator by the same number
- Vice Versa if you’re dividing the 5^ to reduce the exponent, you have to multiple the other denominator factor by the same number

Answer 107

A

Remember what makes positives / negative numbers

Answer 108

A

Look at the answer choices. They are in consective 10 point increments. Work backwards!

Answer 109

A

What is the question asking for?

What is y in terms of x? (i.e. What does y =)
Simplify the quadratic
- The question states that y doesn’t = 4, so eliminate the y-4 possibilites
- Then simplify

Answer 110

A

Work through the quadratics to identify values for each variable

Answer 111

A

Know the geometrical formulas
- Circumference of a circle = 2πr
- Perimeter of square = 4s
- Isosceles triange has a 45: 45: 90 relationship and a x: x: x√2 length relationship

Answer 112

A

Remember to always apply the 10% rule to back into a single digit percent

Answer 113

A

When addressing divisibility problems, remember that in order for something to be divisible by another number, it must contain all of the same prime factors

Answer 114

A

What is the question asking for?

Pay attention to the details. The question identifies that they are consecutive EVEN numbers!

Answer 115

A

Remember that if you have multiple inequalities, you can add them together.

Answer 116

A

Identify how to solve?
- Estimate for each of these fractions
- Remember that a number gets smaller, if the same value is reduced from both the numerator and denominator
  *

Answer 117

A

As the population is doubling every two hours, and the volume listed isn’t too large, you can build a table to back inot the value

You don’t have to solve everything algebraically

Answer 118

A

Anything raised to the power of zero is equal to 1
- Regardless if the numberis negative or positive
Read the question carefully. It’s asking if a number is greater than 1, not greater than zero

Answer 119

A

Remember you’re trying to see if each statement will allow you to solve for the question.

The question asks what is X

Answer 120

A

We need to identify if either p or q is equal to 2

Answer 121

A

In order for an output to be and even number, the numerator must be even

Answer 122

A

Two ways to solve: 1) Back into an answer with the ratios provided, 2) Algebraically. KNOW BOTH

The question identifies that the triangle is right
If it’s a right triangle lean on the pythagorean theorum, to identify the side lengths
- Back into the side lengths by leveraging the ratios provided
Remember the common right triangles: 3:4:5, 5:12:13, 30:60:90, 45:45:90
- If the perimeter equals 4x, and the sides are x,y,z we can high back into a ratio
  - e.g. x =3, 4x = 12, what combination, would allow for 3 + y + z = 12?
    - 3 + 4 + 5 = 12
  - With that in mind, x to y is 3: 4

Algrebraically

We can solve this algebraically, by looking at what we have

We know the Pythagorean theorum: a² + b² = c²
Given: x + y + z = 4x
- z = 4x - (x +y)
- z = 3x - y
Plug this back into pythagorean theorum:
- x² + y² = (3x-y)²
- x² + y² = (3x-y)(3x-y)
- x² + y² = 9x² - 3xy - 3xy + y²
- x² + y² = 9x² - 6xy + y²
- 6xy = 8x²
- 6y = 8x
- x/y = 6/8 = 3/4

Answer 123

A

Look at the answer choices, this is a prime example to work backwards:

You’re given the calories per 3 meals (combined) 2,400
You’re given the snack / dessert intake (combined) 200
- These total to a regular base of 2,600 (2,400 + 200)
Tom splurges on some days eating 3 times snacks / dessert 600 (3 * 200
- Total on these days would be 2,400 + 600 = 3,000
Now you have your regular day totals (2,600) and splurge day total (3,000)

Question is asking how many days did he splurge if his 10 day average was 2,720?

Looking at the answer choices, consecutive singe digit integers
Let’s try the second option, then fourth option to see what works
((2,600 * 6) + (3,000 * 4))/ 10 = 2,760 too big, must be answer A
- Let’s test answer A to confirm
((2,600 * 7) + (3,000 * 3))/10 = 2,720 CORRECT

Answer 124

A

Remember process: Understand, Plan, Solve

Understand: Will Patrick have time to complete task before guests arrive?
Plan: We know he has to:
- Vaccum
- Fold Laundry
- Put away dishes, after Dish Washer completes cycle
- Cycle has 55 minutes remaining, and guests arrive in 1 hour
- In order to solve we need to know how long the tasks will take in total, or if one task would put him over an hour
Solve:
- Statement 1: We have a time value of Vaccuming and Launrdy
  - Without an understanding of how long Dishes will take, this is NS
- Statement 2: We know the cycle will take 55 minutes, then it will take 7 minutes to put dishes away. This is 62 minutes, which exceed an hour, so we know Patrick does not have enough time. Sufficient

Answer 125

A

Understand: How many games were played
Plan: We need need to know what y was and what % that is.

Answer 126

A

Heavy algebraic translation:

You know from the statement that Jennifer has 60 more dollars than brian
- J = B + 60
You also know if she gave him 1/5 of her money Brian would have 25% less than Jennifer
- J - 1/5j = 4/5J
- B = B + 1/5J
  - We can then deduce that b + 1/5j = (1-25%)(4/5j)
  - This simplifies to b + 1/5j = 75%(4/5j)
    - b = 3/5j - 1/5j; b = 2/5j
- Plug this back into the original J = B + 60
  - J = 2/5j + 60
  - 3/5J = 60
  - J = 100

Answer 127

A

Remember to draw the plane
Slope = Rise / run (i.e. vertical over horizontal)
- However, points on a plane are presented (x,y)

Alternatively, you can plug a points coordinates into the equation for a line to see if the coordinates match (i.e. option A coordinates (3,1)

We’re given the equation y = 3x - 8
- If we plug in the (3,1) coordinates we see:
  - y = 3(3)-8 = 1
  - y = 1 in the coordinates given so this works!