Quant Revisit List Flashcards
sqrt(3)
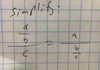
1.7
sqrt(2)
1.4
Put this into an equation:
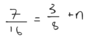
Draw 2 variable + total matrix for this problem:
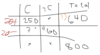
What are the steps to solve:
EASY
Process: 1) split 10 into factors (5*2)^n => (5^n * 2^n) so we have common base 2) solve for n
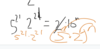
What’s the median and mean for consecutive integers?
2,4,6,8 = MEDIAN=5, MEAN=5; for 1,2,3,4,5,6,7 then MEDIAN=4 and MEAN=4. Middle number is both mean and median.
U got this bro!
Count number of multiples of 3
(Last - First)/(multiple) + 1
How many different ways can you draw an isocolies triangle 40 degree angle?
40,40,100; 40,70,70; etc.
Imagine you’re given a triangle inside a square, if that triangle’s base is the diameter of the circle, and the triangle touches the outside of a circle. What do you know about this triangle?
I know that the triangle has a 90 degree angle at the point that touches the circle.
(x+y)^2
x^2 + 2xy + y^2
(x-y)^2
x^2 -2xy + y^2
How to solve?
SUBTRACT AREAS! will need to create equation using each triangle
((x^5)^4) =
x^20
y^4 * y^9 =
y^13
Sqrt(p*q) =
Sqrt(p)*Sqrt(q)
Even * Odd * Even = ?
Even
Odd * Even * Odd = ?
Even
Factor 147
Methodology: go from smallest to biggest when prime factoring. Clearly not divisible by 2, because 147 is odd.
Next, check for divisibility by 3 – 1+4+7 = 12, so it’s divisible by 3. (or, better, notice that it’s 3 less than the round number 150, which is 3x50, so 147 is 3x49)
How do we tell if something is divisible by 3?
If each digit summed up sums to something that is divisible by three, then the answer is YES.
Example: 147 divisible by 3? Is 3 a factor of 147? 1+4+7 = 12, therefore YES.
Is 0 an integer?
Is 0 even?
YES
and
YES
Zero is both EVEN and an integer.
Is 1 a prime number?
NO!
Are any prime numbers even?
YES! 2 is the ONLY even prime number.
What are the factors of 6?
1,2,3,6
What are the multiples of 6?
6,12,18,24…
How do we tell if a fraction will be finite or repeating?
If denominator as 2 and 5 as prime factors => NOT REPEATING
What is a prime factor?
The prime factors of 15 are 3 and 5 (because 3×5=15, and 3 and 5 are prime numbers).
When X and Y are both positive integers and the remainder is 2:
x/y = integer + remainder / y
This can help solve modulo or remainder questions.
if 0 < x < 1 then rank:
sqrt(x), x^2, and x from least to greatest order
x^2 < x < sqrt(x)
x^2 * y^2 - 16 = ?
(xy - 4)(xy + 4)
x^2 - 9 = ?
(x-3)(x+3)
5/4 = 1 + 1/4
1 is the REMAINDER, the MODULO. Use example to memorize this equation from my intuition.
|2x + 4| = 12, x=?
Solution: Solve the equation TWICE. once for when absolute value is positive, a second time for when it is negative:
POSITIVE:
2x + 4 = 12 therefore x = 4
NEGATIVE
-(2x+4) = 12 therefore x = -8
sqrt(10,000) = ?
100
If two absolute values are equal, what must be true of the expressions?
It must be true that the expressions with the absolute value bars are either equals or opposites.
So:
|expression1 | = |expression2|
becomes in the equals case:
( expression1 ) = ( expression2)
and in the opposite case:
( expression1 ) = -( expression2)
Similar to solving an absolute value, you must solve twice for the unknown
Equation for compound interest:
A = P(1 + r/n)^nt
Remember 5^(x-3) = 5^x / 5^3
this one will be hard to solve w/o paper due to math. But main point is to translate from question to equation DIRECTLY:
A = 0.36*C
Note: translate equations directly from the question.
“mixture weights more than 20 ounces” => m > 20
Property of parallelogram: opposite triangles are the same area. This helps us solve for the isosceles triangle.
Note: it is important to rephrase (a) the information that is given, and (b) the question:
Any scalar => can solve.
GMAT Hack: turn the two digits into variables. Tens digit = 10*A, one’s digit = 1*B.
Note: Translate equations from text!
If y is the smallest positive integer such that 3,150 multiplied by y is the square of an integer, then y must be
(A) 2
(B) 5
(C) 6
(D) 7
(E) 14
True of False: In a perfect square, the prime factors come in pairs
TRUE.
How to tell if divisible by 11?
ex: is 143 divisible by 11?
Units digit and Hundreds digit sum to middle digit:
ex: is 143 divisible by 11?
1+3 = 4, therefore divisible by 11 !
If n=12, how many positive and even divisors does n have, including n?
divisors of 12 = {1,2,3,4,6,12}
even divisors of 12 = {2,4,6,12}
therefore, 4.
the diagram is wrong. answer should read:
2^2 + 2(2) + 1 = (2+1)(2+1) = 3*3* = 9
How do we know the area of an obtuse triangle?
still (1/2)*b*h, however the height is from the triangle that forms a right angle (see photo–blue triangle)
If a given triangle has two sides taht are the same length, is it isocolies?
YES. and the two opposite angles are both the SAME angle as well.
This problem, for example, can’t be solved without knowing this:
How many 2 person teams can be formed with persons 1,2,3,4,5,6,7, and 8?
8 choose 2 =
n! / ((n-k)! k!)
8! / ((8-2)! * 2! )
8*7 / 2
56 /2
28.
NOTE: team “1,2,3” is same as “3,1,2” and “2,1,3” therefore order doesn’t matter. This is why we use COMBINATIONS equation.
