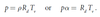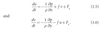part 1 Flashcards
Synoptic meteorology
meteorology traditionally involves the study of weather systems, such as
- extratropical high and low pressure systems,
- jet streams
- associated waves
- fronts.
mesoscale meteorology
- the study of convective storms,
- land–sea breezes,
- gap winds,
- and mountain waves
The earth system exhibits a continuous……………………….spectrum of motion that defies simple categorization.
spatial and temporal
Weather forecasting
necessitates understanding a wide range of processes and phenomena acting on a variety of spatial and temporal scales.
forecasting for a coastal location requires information concerning
- the near-shore water temperature,
- the potential for land–sea breeze circulations,
- and the strength and orientation of the prevailing synoptic-scale wind flow.
The prediction of precipitation type can benefit from
knowledge of atmospheric thermodynamics and cloud physics.
Other types of prediction, including ……………………………………… and ……………………………, also require knowledge that spans a broad spectrum of meteorological processes.
air quality forecasting and seasonal climate prediction
quasigeostrophic (QG) equations
simplified version of the full primitive equations
igoners small terms
momentum equations are
continuous
ideal gas
hydrostatic
geostraphic wind is a balance between
corriolis and PGF
scale analysis
a systematic strategy to determine which terms in the equations, often associated with specific physical processes, are most important and which are negligible in a given meteorological setting.
scale analysis is a systematic strategy to determine which terms in the equations, often associated with specific physical processes, are most important and which are negligible in a given meteorological setting. By
characterizing the temporal and spatial scales associated with specific weather systems, we can systematically neglect “small” terms in the governing equations in the study of those systems.
for synoptic- and planetary-scale weather systems, such as cyclones and anticyclones, we know that in the ……………………………, flow above……………………tends to be fairly close to a state of ……………………………balance
midlatitudes, ~1 km altitude, geostrophic
—flow above ~1 km altitude tends to be fairly close to a state of geostrophic balance, whereas for mesoscale weather systems, such as thunderstorms, it …………………………………………………….
does not, even in the same geographical location
geostrophic balance ignores
friction
whereas for mesoscale weather systems, such as thunderstorms, it does not, even in the same geographical location. Why?
cannot ignore friction
This is one example of why students in the atmospheric sciences are required to derive equations, because it is important to know what ……..
- assumptions were made in the development of a given technique
- this information is needed to deduce which tools are appropriate for which situations.
- the ability to apply a systematic approach to the governing equations allows atmospheric scientists to develop new equations and techniques to study unique problems.
The length scale can be related to
the size of a weather system, or how far an air parcel would travel within the system during a given time interval.
The time scale
can be related to how long it would take an air parcel to circulate within the system
Scale: Microscale
length:
less than 1 km
Scale: Microscale
time:
less than 1 hour
Scale: Microscale
example phenomena:
Turbulence, PBL
Scale: Mesoscale
Length:
1 - 1000 km
Scale: Mesoscale
time:
1 h - 1 day
Scale: Mesoscale
example phenomena:
Thunderstorm, land-sea breeze
Scale: synoptic
length:
1,000-4,000
Scale: synoptic
time:
1 day-1 week
Scale: synoptic
Example phenomena:
Upper level trough, ridges, fronts surface lows and highs
Scale: Planetary
Lenght:
less than 4000 km
Scale: planetary
time:
less than 1 week
Scale: planetary
Example phenomena:
polar front jet streams, trade winds
the dependent variables in the system
- the four independent variables are the three spatial directions
- and time, denoted as x, y, z, and t, respectively
governing equations are applied to a flat “cartesian” earth for
- qualitative work,
- or if we study weather systems that are sufficiently small in spatial scale, we can neglect the distortion that results.
shows unit vectors in an orthogonal Cartesian coordinate system. For some applications, the i and j unit vectors may be
grid relative
the horizontal coordinate directions here will be taken to align with
latitude and longitude lines
A and B represent
K^ (z, + upward)
C and D represent
j^ (y, +northward)
E and F represent
i^ (x, +eastward)
omega = dp/dt is (…..) upward
negative
w=dz/dt is (…….) upward
positive
a variety of vertical coordinates measures are used in place of the ……….
vertical distance z
a variety of vertical coordinate measures are used in place of the vertical distance z to determine …..
determine position along the vertical coordinate axis
popular choice of vertical coordinates
pressure, sigma (a terrain-following ratio of pressure to surface pressure), potential temperature, or a hybrid among these
the k unit vector maintains
right angles with the horizontal unit vectors.
vertical coordinates are known as……
isobaric coordinates
an important practical advantage is that historically, it was easier to measure ……………………………. than ……………………….for in situ measurements taken aloft.
pressure than altitude
a rawinsonde can measure
pressure with a baroswitch
aircraft are designed to measure
pressure and fly along surfaces of constant pressure
The wind velocity components are based on
the time rate of change in the distance along the respective coordinate axes following the airflow
Wind velocity components (equations)
The following are the
wind velocity components
dx/dt indicates
change in zonal (east–west) distance
dx/dt is positive for motions toward the…..
east
dy/dt indicates
meridional (north - south)
dz/dt indicates
vertical components
omega is
the vertical motion in isobaric coordinates
omega (ω), is defined as
the following equation represents
omega
Omega, The pressure-coordinate vertical velocity is ………………….for upward motion
negative
The pressure-coordinate vertical velocity is negative for upward motion, because
pressure decreases with height
notations for the 2D horizontal and 3D wind vectors
the following represents
notations for the 2D horizontal and 3D wind vectors
the following equations indicate the
direction
Coriolis parameter is related to
the projection of the earth’s rotation onto the vertical (kˆ) axis
coriolis parameter is given by
f = 2Ωsin ϕ
the following is the
f = 2Ωsin ϕ
corriolis parameter
corriolis is ……. over the equator
zero
explain each term in the “corriolis parameter”
latitude is denoted ϕ and Ω is the earth’s rate of angular rotation, 2π radians day–1, with a day here being the sidereal day (23 h 56 min).
The numerical value of Ω is 7.292x10−5 rads−1.
basic variables include
pressure (p), temperature (T), density (ρ), and specific volume (α= 1/ρ ).
density is defined as
the mass of air m per unit volume, a cubic meter
dewpoint (Td) is the
Measures of absolute water vapor content
specific humidity (q), and mixing ratio (r) are similar in
magnitude
specific humidity (q) is the
mass of vapor per unit mass (kg) of air mv/m
mixing ratio is given by
the mass of vapor per unit mass of dry air, mv/md.
Values of the mixing ratio and specific humidity can be defined for
saturated conditions
relative humidity is
A measure of the degree of saturation
Unless otherwise stated, the units to be used in this text are those of the System Internationale (SI), which is summarized in Table 1.2. The only frequent exception in this text is
- millibar (mb), equivalent to the hectopascal (hPa, or 100 Pa)
- degrees Celsius (°C), which are equivalent in size to kelvins (K)
Quantity: length
Unit:
SI unit and notation:
Meter
m
Quantitiy: time
Unit:
SI unit and notation:
second
s
Quantitiy: Mass
Unit:
SI unit and notation:
Kilogram
kg
Quantity: Temperature
Unit:
Si units and notation:
Kelvin
K
Quantity: Velocity
Unit:
SI units and notation:
Meter/second
m/s
Quantity: force
Unit:
SI units and notation:
Newoton
N (kg m/s2)
Pressure
Unit:
SI unit and notation:
(force/area)
pascal
Pa (Nm2 or kg/m s)
energy or work
unit:
SI units and notation
Joule
J(Nm or kg m2/s2)
the ideal gas law is also known as
equation of state
the ideal gas law
provides a useful relation between the pressure, temperature, and density
The ideal gas law equation
the following equation is for
ideal gas law
explain each term in the equation
Rd is the dry-air gas constant
Tv is the virtual temperature ( The temperature that a parcel of dry air would have if it were at the same pressure and had the same density as moist air. )
Tv= T (1+0.61q). Rd = 287 J/ kg.K.
The momentum equations in Cartesian form
