Other demand topics

Question 1

Changes with excess demand funcition

Answer 1

z(p)=x(p,p*endowment)-endowment

z(p) is homogeneous of degree zero

walras law becomes pz(p)=0

Slutsky equation

Question 2

complete and credit markets

Answer 2

(x1,x2) is reachable with complete prices at prices (p1,p2) iff it is reachable in spot markets with credit market at prices (p1,p2(1+i))

Question 3

real interest rate

Answer 3

q1(1+i)/q2

Question 4

Composite good theorem first stage

Answer 4

• u continuous
• Strictly quasiconcave
• increasing
• relative price of the goods of the bundle is fixed and strictly positive

Then

• First stage problem has a unique solution x_2(x1,w_2;p_2)
• v(.) is continuous in (x_1,w_2)
• v(.) is strictly quasiconcave in (x_1,w_2)
• v(.) is increasing in (x_1,w_2)

Question 5

composite good theorem second stage

Answer 5

Under the assumptions of the first stage and for any (p1,theta,w)>>0, the second stage has a unique solution and this solution is the same as the one that one can get with the one stage problem

Question 6

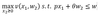
Definition of reservation wage

Answer 6

maximum salary with which I don’t work

Question 7

Definition of CV and EV

Answer 7

Assumptions: preferences are continuous, LNS, strictly quasiconcave and differentiable) then:

CV=w-e(p_1,u_0)

EV=e(p_0,u_1)-w

Question 8

Properties of CV and EV

Answer 8

• CV>=0 iff EV>=0 iff U1>=U0
• p0, p1, p2, then p2 is prefered to p1 iff EV(p0,p2)>=EV(p0,p1)
• For normal goods EV>=S>=CV
• For inferior goods EV<=S<=CV
• Equality is attained iff there are no wealth effects

Question 9

property homothetic pref

Answer 9

the preferences are homothetic iff there is a continuous utility function that is homogeneous of degree one

Question 10

property quasiliear preferences

Answer 10

preferences are quasilinear iff there is a quasilinear utility function that represents those preferences

quasilinear utility functions give rise to v(p,w) quasilinear in w and e(p,u) quasilinear in u

Wealth expansion paths are parallel with respect to the access of “quasilinear” good

Question 11

Quasihomothetic preferences

Answer 11

If they induce expenditure functions of the gorman form:

e(p,u)=a(p)+ub(p)

This implies

• v(p,w) and hicksian demands are also of the gorman form
• Expansion paths are straight lines
• Homothetic and quasilinar preferences are particular cases of quasihomothetic ones

Question 12

Independence of aggregate demand from wealth distribution

Answer 12

• This happens iff the marginal propensity to consume of every single good with respect to wealth is the same for all consumers and for any wealth level.
• The aggregation if feasible iff all consumer have quasihomothetic preferences with the same b(p)