Demand theory Flashcards
(19 cards)
Homothetic preferences
Monotone
If x~y ⇒ ax~ay, a>0
Debreu’s theorem
If the preferences are continuous and rational, then there is a continuous utility representation
Existence of walrasian demand
- Continuous preferences
- Prices strictly positive
Then
- Utility maximization problem has a solution
Uniqueness of Walrasian demand
Uniqueness
- Continuous preferences
- Prices strictly positive
Then
- Utility maximization problem has a solution and it is unique and x(p,w) is a function
Walras law
- U continuous
- Locally nonsatiated
- p>>0
- w>=0
Then
px(p,w)=w
Homogeneity of walrasian demand
Walrasiand demand is homogeneous of degree zero
Properties of v(p,w)
- u continuous and locally
- LNS
Then v(p,w)
- homogeneous of degree zero in (p,w)
- non decreasing in p and strictly increasing in w.
- continuous in (p,w)
- quasiconvex in (p,w)
Existence of hicksian demand
- U continuous
- p>>0
Then expenditure minimizarion problem has a solution
Uniqueness of hicksian demand
- U continuous
- p>>0
- u strictly quasiconcave
Then h(p,u) is unique and continuous,
analogous of walras law for e(p,u)
- U continuous
- p>>0
Then
u(h(p,u))=u
Homogeneity of the hicksian demand
hicksian demand is homogeneous of degree zero in p
Compensated law of demand
- u continous
- h(p,u) is a function
then for all p’, p’’>>0
(p’-p’’)(h(p’)-h(p’’))<=0
e(p,u) properties
- u continuous
- LNS
- p>>0
Then e(p,u)
- homogeneous of degree 1 in p
- concave in p
- strictly increasing in u and not decreasing in p
- continous in (p,u)
duality
- u continuous
- p>>0
- LNS
Then
- x solves UMP for w>0 then x solves EMP for u=u(x)
- x solves EMP for u>u(0) then x solves EMP for w=px
Shepard’s lemma
- u continous
- strictly quasiconcave
- LNS
then
- e(p,u) is continuously diff at p>>0.
- Dpe(p,u)=h(p,u)
Roy’s identity
- u continous
- strictly quasiconcave
- LNS
- v(p,w) is diff at (p,w)>>0
Then
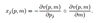
Slutsky equation
- u continuous
- strictly quasiconcave
- LNS
- x, h diff
Properties of S
- u continuous
- strictly quasiconcave
- LNS
- h is C1
then for all (p,w)>>0
- S is the hessian of e(p,u)
- S is negative semidefinite
- S symmetric
- Sp=0
Integrability
If we gave a rational consumer satisfying LNS with diff walrasian demand x(p,w)
- px=w
- x(p,w) is homogenous of degree 0 in (p,w)
- S(p,w) is symmetric and negative semidefinite and S(p,w)=0
If the demands satify the above mentioned properties then they can be rationalized by means of a preference relation.


