Mechanics; Torsion Flashcards
_______ refers to the twisting of a straight bar when it is loaded by a _______ (or torque) that tends to produce _______ about the longitudinal axis of the bar. Provide examples of rotation
Torsion
moment
rotation
Examples: Drive Shafts, axles, propeller shafts, steering rods, drill bits, screw driver
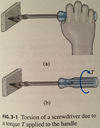
Typical USCS units for moments are the ____-_____ & ______-_______.
Typical SI unit for moments is the _____-____.
lb*ft
lb*in
N*m (Newton-meter)
SI= International System of Units
USCS= United States Customary System
Moment vectors that produce twisting of a bar, such as moments T1 and T2 on figure 3-2 are called ______, or _____ _____.
torques
twisting moments
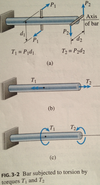
Definition for shafts
Cylindrical members that are subjected to torques and transmits power thru rotation.
Each pair of forces forms a ____ that tends to twist the bar about its longitudinal axis.
couple
As we know from statics, the _____ _____ ____ _____ is equal to the product of 1 of the forces and the ____ ____ between the lines of action of the forces.
moment of a couple
perpendicular distance
The moment of a couple may be represented by a _____ in the form of a double-headed arrow.
vector
The direction (or sense) of the moment is indicated by the ____ _____ _____ for moment vectors.
right hand rule
Draw Diagram for Deformation of a Circular Bar in Pure Torsion-
A prismatic bar of circular cross section twisted by torques (T) acting at ends. Every cross section of the bar is identical. Every cross section is subjected to the same internal torque (T). This bar would be considered to be in _____ _____.
Pure Torsion
_____ is known as the ____ ____ ____, or angle of rotation. Reference the attached figure showing pure torsion and angle of twist.
φ (Greek letter phi)
angle of twist
For Pure torsion only, Rate of Twist=
Shear strain max formula for Torsion-
Rate of Twist= Angle of twist/ Length
See Image
γ = Shear strain; (Greek letter Gamma)
r = exterior radius
φ = angle of twist (Greek Letter Phi) θ= rate of twist (Greek Letter Theta) L= Length
Draw Diagram for Shear Strain in a Circular Tube
Shear Strain formula for Torsion for interior elements
γ= ρθ = (ρ/r)* γ(max)
γ= Shear strain; (Greek letter Gamma)
r= exterior radius
ρ= interior radius (Greek Letter Rho)
θ= rate of twist (Greek Letter Theta) L= Length
Draw Diagram for Shear Stresses in Torsion of a Circular Bar
Torsional shear stress at a distance p from the center of the bar is ____ (Equation) This equation expands out further from Torsion Formula.
τ = Gρθ = (ρ/r)*τmax = (Tρ)/Ip
τ = Shear stress; (Greek letter Tau)
G= Shear Modulus of Elasticity
T= Torque
Ip= Polar Moment of Inertia
r= exterior radius ρ= interior radius (Greek Letter Rho)
θ= rate of twist (Greek Letter Theta)
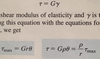
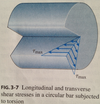
Draw 3D Diagram of Longitudinal and Transverse Shear stresses in a Circular Bar subjected to Torsion
Max torsional shear stress for both solid bars & circular tubes is _______ (equation) This equation expands out further from Torsion Formula.
τ (Max)= Grθ = (T*r)/Ip
τ = Shear stress; (Greek letter Tau)
G= Shear Modulus of Elasticity
T= Torque
Ip= Polar Moment of Inertia
r= exterior radius
θ= rate of twist (Greek Letter Theta)
Torsion Formula= (T*r)/Ip
Draw Picture for the determination of the resultant of the shear stresses acting on a cross section
What is the Polar Moment of Inertia (Integration) formula- What is the Polar Moment of Inertia for a Circle of radius r, and diameter d?
Refer to Picture
Max torsional shear stress for both solid bars & circular tubes is _______ (equation) Include formulas from previous Section- What is the Torsion Formula (equation)?
τ (Max)= Grθ = (T*r)/Ip
τ = Shear stress; (Greek letter Tau)
G= Shear Modulus of Elasticity
T= Torque
Ip= Polar Moment of Inertia
r= exterior radius
θ= rate of twist (Greek Letter Theta)
Torsion Formula= (T*r)/Ip
Max Shear stress for Torsion for solid circular cross section; Provide equation
τ (Max)= (16*T)/(π*d^3)
τ (Max)= Shear Max for a solid circular cross section
T= Torque
d= diameter
Torsional shear stress & distance p from the center of the bar is ____ (Equation) Include formulas from previous Section
τ = Gρθ = (ρ/r)*τmax = (Tρ)/Ip
τ = Shear stress; (Greek letter Tau)
G= Shear Modulus of Elasticity
T= Torque Ip= Polar Moment of Inertia
r= exterior radius ρ= interior radius (Greek Letter Rho)
θ= rate of twist (Greek Letter Theta)
Equation for Rate of Twist & Angle of Twist of a bar of linear elastic material-
For a bar in pure torsion, the total angle of twist (φ), equals to the rate of twist times the length of the bar.
Provide equation-
Rate of twist is measured in ?
Angle of Twist is measured in ?
θ= T/(G*Ip); Measured in units of radians per unit Length
θ= Rate of Twist (Greek Letter Theta)
φ= TL/(G*Ip) Measured in radians
φ= Angle of Twist (Greek Letter Phi)
T= Torque
G= Shear Modulus of Elasticity
Ip= Polar Moment of Inertia
L= Length of member
G*Ip is known as the _____ ____ of the bar.
Torsional Rigidity
The torsional stiffness of a bar is the _____ required to produce a unit angle of rotation. Provide equation:
The _____ _____ is the reciprocal of the stiffness (k), and is defined as the _____ ____ _____ produced by a unit torque. Provide equation
Torque
k = (G*Ip)/L k= Stiffness
Torsional Flexibility
f= L/(G*Ip) f= Flexibility
Circular tubes are more _____ than solid tubes in resisting torsional loads. Analysis of the torsion of a circular tube is almost identical to that of a _____ _____.
Provide Polar Moment of Inertia for the cross sectional area of a tube.
efficient
solid bar
Ip= (π/2)*(r2^4 - r1^4) Or
Ip= (π/32)*(d2^4 - d1^4)
d= diameter
r= radius
_____ _____ refers to torsion of a prismatic bar subjected to torques acting only as the ends.
Pure torsion
___ ____ differs from pure torsion in that the bar need not be prismatic, and the applied torques may act anywhere along the axis of the bar.
nonuniform torsion
Bars in nonuniform torsion can be analyzed by applying the formulas of ____ ____ to finite segments of the bar, and then adding the results.
pure torsion
The most important use of Circular shafts is to _____ _____ _____ from one device or machine to another, as in a drive shaft of a car, propeller shaft of a ship, or axle of a bike.
transmit mechanical power
The greek letter for Angular Speed is ____, measured in ____/____.
ω (Omega)
radians / second
Equation for work done by a torque of constant magnitude.
W= T*Ψ
W= Work
T= Torque
Ψ= Angular Displacement (Greek Letter Psi)
____ is the rate at which work is done.
Power
P= dW/dt = Tω = 2πfT = (2πnT)/60
P= Power
W= Work
T= Torque
ω= Angular Speed (Greek Letter Omega; measured in rad/sec)
f= frequency (f= Hz= s^-1)
n= number of revolution per minute (RPM)
The power formula, (P=T*ω), give the power transmitted by a rotating shaft transmitting a constant ______.
Torque (T)
Angular Speed equation
ω= 2πf
ω= Angular Speed (Greek Letter Omega)
f= Frequency (Italic f)
If torque is expressed in Newton Meters, then the power is expressed in _____.
watts (W)
One Watt is equal to ____ ____ ____ ____ ____.
1 Newton Meter per second (or 1 Joule per second)
If Torque is expressed in pound-feet, then the power is expressed in ___ ____ ___ ___.
foot pound per second
Angular Speed is often expressed as the ____ of rotation, which is defined as
frequency (f)
Number of revolutions per unit of time
The unit for frequency is the _____.
hertz (HZ)= S^-1
One revolution = _____
2*π radians
Equation for Power
P= dW/dt = Tω = 2πfT = (2πnT)/60
P= Power
W= Work
T= Torque
ω= Angular Speed (Greek Letter Omega)
f= frequency (f= Hz= s^-1)
n= number of revolution per minute (RPM)
In U.S. Engineering practice, power is sometimes expressed in ___, a unit equal to _____.
Provide Equation
horsepower (abbreviated H)
550 ft*lb
H= (2πnT)/60 = (2πnT)/(60*550) = (2πnT)/33,000
H= Horsepower
n= Number of revolutions per minute (RPM)
T= Torque
1 horsepower = ______ watts.
746
_____ are structural members subjected to ____ loads, that is, forces or _____ having their vectors perpendicular to the axis of the bar.
Beams
lateral
moments
What is a simply supported beam
A beam with a pin support @ one end & a roller support @ the other end.
The essential feature of a pin support is that it prevents _____ at the end of a beam, but does not prevent ______.
translation
rotation
A roller support prevents translation (movement) in the _____ direction, but not in the _____ direction.
vertical
horizontal
A BEam to Column Support such as the one pictured would be considered a ______ support?
Pin
A beam to column connection in which a beam is attached to a column flange by bolted angles. This type of support is usually assumed to restrain the beam against horizontal movement, but not again rotation (restraint angle rotation is slight because both the angles and the column can bend). Thus this connection is usually represented as a pin support for the beam.
Sign conventions for positive shear force (V) & positive bending moment (M).
Draw Diagram
The shear force tends to rotate the material ____ and the bending moment tends to _____ the upper part of the beam, and _____ the lower part.
Clockwise compress elongate
Sign conventions for stress resultants are called _____ _____ _____ because they are based upon how the material is deformed.
deformation sign conventions
Image for a Composite Beam
Explain the Calculation Procedure for Composite Beam Analysis-
Composite Beams;
Read Example and make sure concept is understood
GIVEN: A nominal 6x10 wood beam (actual dims 5½” x 9½”) is reinforced with a
5½” x ½” plate at the bottom to form a composite flitch beam. Use 1,500,000 psi
for the modulus of elasticity of the wood and 29,000,000 psi for the steel.
