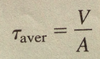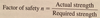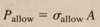Mechanics; Chapter 1 Flashcards
Define the Term “Free Body Diagram”
A sketch of the structure, removed from it’s supports, showing all dimensions, applied forces, and reactions.
Chapter 1
Define a “brittle material”-
A material that fractures w/o significant strain such that there is no noticeable deflection before fracture occurs.
Chapter 1
Define the term “stiffness”-
Stiffness is the force required to cause a unit displacement in a linear elastic member. (K=P/δ)
Chapter 1
Define the term “Flexibilty”-
Flexibility is the amount of deformation caused by a unit force in a linear elastic member.
Chapter 1
Define a “determinate” structure-
A Determinate Structure is one that has the same number of unknown reactions as the number of applicable equations of static equilibrium.
Chapter 1
Greek Alphabet
Chapter 1
Define Prismatic Bar
A straight structural member having the same cross section throughout its length.
Chapter 1
Define Axial Force
A load directed along the axis of a member, resulting in either tension or compression in the member.
Chapter 1
Define Cross Section
A section taken perpendicular to the longitudinal axis of a member.
Chapter 1
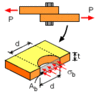
Define Stress (Mechanics of Material)
Intensity of a force (Force per unit Area); Denoted by the greek letter Sigma (σ)
Mechanics of Materials
Define Normal Stress
Stress that act in a direction perpendicular to the cut surface.
σ=P/A
σ= Normal Stress;
P= Axial force;
A= cross-sectional area
Chapter 1
Mechanics of Material; Because normal strain is a ratio of 2 lengths, it is a _____ ______.
Dimensionless quantity
Chapter 1
Sign Convention for Tensile Stress & Compressive Stress
Tensile Stress= Positive Compressive Stress= Negative
Chapter 1
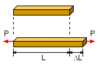
Normal Strain equation-
Elongation per unit length-
ε= δ/L; Epsilon=Delta/Original Length
ε = ΔL/L
Chapter 1
The elongation of the bar is assumed normal, or perpendicular, to the cross section.
Normal Strain (Continued)
Chapter 1
A _____ is a device that is used to measure changes in lengths of an object. Is is useful for the stress/strain measurements & tensile test.
Extensometer
Mechanics
The ASTM standard tension specimen has a diameter of ___ in. and a gage length of ___ in. between the gage Marks, which are the points where the extensometer arms are attached to the specimen.
.505 inch
2 inch.
Chapter 1
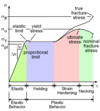
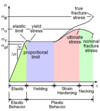
The ______ ______ is the point where the material changes from linear to non-linear on the stress/strain diagram.
proportional limit
Chapter 1
Explain Stress Strain Diagram
Elastic Range; Yielding; Strain Hardening; Necking
Chapter 1
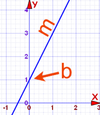
Explain how the Equation of a line is used in Mechanics of Material
y = mx + b ;
y = how far up;
x = how far along;
m=Slope (Rise/Run);
b = the Y Intercept (where the line crosses the Y axis).
This equation can be substituted into the stress/strain diagram to solve problems. σ = E * ε + B
Chapter 1
Define a Ductile Material
Metals such as structural steel that undergo large permanent strains before failure.
Chapter 1
Structural Steel is also know as-
Mild Steel Low-Carbon Steel
Chapter 1
When a material such as aluminum does not have an obvious yield point and yet undergoes large strains after the proportion limit is exceeded, and arbitrary yield stress may be determined by the _____ _____.
offset method
Chapter 1
For the offset method, a straight line is drawn on the stress-strain diagram parallel to the initial linear part of the curve, but offset by some standard strain, such as _____ of (___%)
.002 2%
Chapter 1
Staying in the Linear elastic region of the stress vs strain diagram will avoid _______ ______ when loads are removed.
permanent deformation
Chapter 1
Explain Hooke’s Law?
F = kδ
σ = Eε or E= σ/ε
E is the material property that represents the stiffness of the material (called Young’s Modulus).
Chapter 1
Through experiments, it can be shown that most materials act like springs in that the force is proportional to the displacement (δ). However, unlike a spring, a bar has a cross-sectional area that effects the displacement. Therefore, it is simpler to relate the stress (F/A) to the strain (δ/L). This gives the relationship, PL/AE The linear relationship between stress (σ) and strain (ε) for a bar in simple tension or compression.
Chapter 1
Modulus of Elasticity (E) is the _____ of the stress-strain diagram in the ____ _____ region.
slope
linear elastic
Chapter 1
The ratio of the lateral strain being directly proportional to the axial strain is known as _____ _____.
Poisson’s Ratio;
ν=-ε’/ε;
ε’= lateral strain
ε= axial strain;
Chapter 1
When a prismatic bar is loaded in tension, the axial elongation (ε) is accompanied by _____ _____.
Lateral Contraction (ε’);
(Contraction normal to the direction of the applied load)
Chapter 1
The _____ _____ at any point in a bar is proportional to the axial strain at the same point if the material is ________.
Lateral Strain
Elastic
Chapter 1
Average Bearing Stress Equation
σb = Fb/Ab;
Fb= Total bearing force
Ab= Bearing area defined as the projected bearing area.
Chapter 1
Define Shear Stress
Stress that acts tangential to the surface of a material.
Chapter 1
Average Shear Stress Equation-
Average Shear stress = Total Shear divided by the cross sectional area.
Chapter 1
The _______ shear stress is obtained by diving the total _____ _____ by the area of the _____ _______ on which it acts.
average
shear force
cross section
Chapter 1
Example of Shear Loading on a Bolt Shear Loading on a Bolt
Chapter 1
Example of Shear Loading on a Lap Joint Shear
Materials
Example of Shear Loading on a Plate Shear Loading on a Plate
Chapter 1
What is the equation for Hooke’s Law in Shear?
G = τ/γ
G= Shear Modulus of Elasticity
τ = Shear stress (Tau)
γ =Shear Strain (Gamma);
The shear strain is defined as the angle (radians) caused by the shear stress as shown in the diagram.
Mechanics of Material
What is the equation for Shear Modulus of Elasticity?
G = E / 2(1 + ν)
G = Shear Modulus of Elasticity
ν = Poissons Ratio (Greek Letter Nu)
E = Modulus of Elasticity
Chapter 1
What is factor of safety? Provide basic equation-
Factor of safety (n) is the ratio of the actual strength to the required strength. n=Actual Strength/ Required Strength
Chapter 1
What is Margin of Safety?
Provide equation-
In aircraft design it is customary to speak of Margin of Safety which is Factor of Safety minus 1.
Margin of Safety= n-1
Chapter 1
When a factor of safety is applied with respect to the yield stress, we obtain a ____ ____ or (_____ _____) that must not be exceeded anywhere in the structure. Provide Equation-
allowable stress
working stress
Allowable stress= Yield strength/factor of safety
Chapter 1
Allowable Load=
Allowable Load= Allowable Stress * Area P(allow)=σ(allow)*A
