Mechanics & Structures Basic Equations

Question 1

Provide Equation for Stress for an Axial Loaded Member

Answer 1

axial stress is equal to the axial force divided by the cross setional area

Question 2

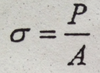
Provide Equation for Strain for an Axial Loaded Member

Answer 2

Axial Strain (Epsilon) is equal to the elongation (delta) divided by the origional length

Question 3

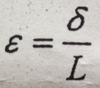
Provide Equation for Modulas of Elasticity (Hooks Law) for an Axial Loaded Member

Answer 3

Modulas of Elastcity (Youngs Modulas) is equal to the axial stress divided by the axial strain

Question 4

Provide Equation for Elongation for an Axial Loaded Member

Answer 4

The elongation of an axial loaded memer is the summation of all applied loads times the lengths of the members divided by the cross sectional area time the modulas of elasticy of the members.

Question 5

Provide Equation for Poison’s Ratio for an Axial Loaded Member

Answer 5

Poson’s Ratio is the laterial strain divided by the axial strain. The lateral strain is negative becasue al the member is elongated, the cross section area become decreased. This is proportional for a linear elastic member (a memeber in the Hook’s Law Portion.

Question 6

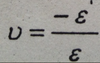
Provide equation for elongation due to temperature change in an Axial Loaded Member

Answer 6

Elongation is equal to the coefficient of thermal expansion time the change in temperature time the origional length of the member

Question 7

Provide equation for Torsional Shear Stress for Torsion/Power Design?

Answer 7

Torsional Shear stress from the Torsion Law is eqaul to the appltied Torque time the radius where the shear will be measured divided by the polar moment of Inertia.

Question 8

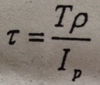
Provide equation for Angle of Twist for Torsion/Power Design?

Answer 8

The angle of twist for a member in torsion is equyal to the Torque applied to the member time the orional length of the member divided by the shear modular of elasticity time the polar moment of inertia.

Question 9

Provide equation for Power for Torsion/Power Design?

Answer 9

Power is equal to Torque times the angular Velocity

Question 10

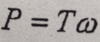
Provide equation for Angular Velocity for Torsion/Power Design?

Answer 10

Angular Velocity is equal to 2 times pi times the frequency

Question 11

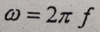
Provide equation for Torsional Shear Strain for Torsion/Power Design?

Answer 11

Torsional Shear Strain is equal to the radius where the strain will be measured time the angle of twist divided by the origional length of the member

Question 12

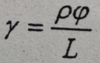
Provide equation for Shear Modulas of Elasticity for Torsion/Power Design?

Answer 12

Shear Modulas of Elasticity is equal to the shear stress divided by the shear strain

Question 13

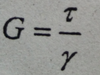
1 horsepower= ____ ft-lb/s?

Answer 13

1 horsepower is equal to 550 ft-lb/s?

Question 14

Polar Moment of Inertia for a circle

Answer 14

Polar Moment of Inertia for a circle is equal to pi time the radius raised to the 4th power divided by 2 of pi time the diameter raised to the 4th power divided by 32

Question 15

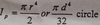
Moment of Inertia for a circle

Answer 15

The moment of inertia for a circle is equal to pi time the radius raised to the 4th power divided by 4 or pi times the diameter raised to the 4th power divided by 64

Question 16

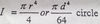
Moment of Inertia for a rectangle

Answer 16

The moment of inertia for a rectangle is equal to the base time the height raised to the 3rd power divided by 12

Question 17

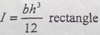
What is the equation for the Parallel Axis Theorem & what is it used for

Answer 17

The equation for the parallel axis theorem is the summation of the moment of inertia plus the area times the distance from the area of concern to the centroid of all members squared

The Parallel axis theorem is used for finding the moment of Inertia.

Question 18

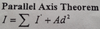
Provide Equation for Bending Stress for a Beam

Answer 18

The bending stress for a beam is equal to the moment time the centroid of the beam divided by the moment of inertia. Since section modula is equiviant to the moment of inertia divided the the centroid the equation for the bending srress for a beam becomes the moment divided by the section modulas of the member.

Question 19

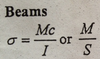
Provide Equation for Shear in a rectangular Beam, and explain what Q means

Answer 19

Shear in a rectangular beam is equal to the shear srtress time the summation (Ay) of the area above the plane of interest divided by the moment of inertia times the base width

Question 20

Blank

Question 21

Explain the equations for Basic Column Design for Compression members with Compact & Noncompact sections

Answer 21

φPn ≥ Pu Pn=Nominal Compressive Strength Pn=Fcr*Ag = Limit state of Flexural Buckling Fcr= Flexural Buckling Stress Fe= Elastic Critical Buckling Stress r= Governing Radius of Gyration K= Effective Length Factor φ= 0.9 for LRFD (Safety Factor)

Question 22

Provide Equations for Steel and Reinforced Concrete Beam Design

Answer 22

Refer to Image

Question 23

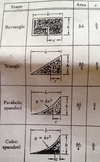
What is the area and where is the centroid for a rectangle, Triangle, Parabolic spandrel, and cubic spandrel?

Answer 23

Refer to Image

Question 24

What are the 3 basic load combinations for design.

Answer 24

Refer to Image

Question 25

Explain the knowns to unknows for statically determinate/indeterminate behavior

Answer 25

Refer to Image

Question 26

Explain procedure for determining if a Beam is statically determinate or indeterminate by the number of unknows versus knowns

Answer 26

Refer to Image

Question 27

Explain procedure for determining if a Frame is statically determinate or indeterminate by the number of unknows versus knowns

Answer 27

Refer to Image

Question 28

Explain procedure for determining if a Truss is statically determinate or indeterminate by the number of unknows versus knowns

Answer 28

Refer to Image

Question 29

Provide and explain equation for Virtual Work for Flexural Forces

Answer 29

Refer to Image

Question 30

Provide and explain equation for Virtual Work for Axial Forces

Answer 30

Refer to Image