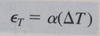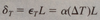Mechanics; Chapter 2 Flashcards
Structural Components subjected to tension or compression are know as ____ _____ members.
axially loaded
When determining the changes in lengths of axially loaded members, it is convenient to begin with a ______ ______, since the overall stretching or shortening is analogous to the behavior of a bar in tension or compression.
coil spring
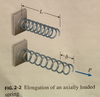
The natural length is also called the ____ _____ (3 different names).
unstressed length
relaxed length
free length
When applying a tensile load to a spring, the spring lengthens by an amount _____ and its final length becomes ______ + ______.
δ
L + δ
L= original length)
δ= (Greek Letter Delta)= elongation or uniaxial deflection;
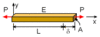
Define Stiffness for a Spring Provide Equation
Defined as the force required to produce a unit elongation in a linear elastic member
k = P/δ
k=stiffness
p= axial force
δ=elongation
Define Flexibility for a Spring Provide Equation
Defined as elongation produced by a load unit value.
f = δ/P
f=flexibility
p=axial force
δ=elongation (Greek Letter Delta)
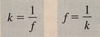
Stiffness and flexibility of a spring are ______ of each other.
reciprocals
k=1/f
f=1/k
k= Stiffness
f= flexibility
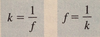
Flexibility of a spring can easily be determined by measuring the _____ produced by a know load.
elongation (δ)
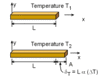
When a prismatic bar of linear elastic material is loaded ONLY at the ends, we can obtain its length from the equation ______.
δ=PL/AE
δ= Elongation (Greek Letter Delta)
P= Axial force
E= Modulus of Elasticity
L= Length
A= Cross Sectional Area
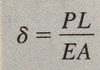
Explain how the equation for Uniaxial Deflection is derived
For a simple homogenous bar with a constant cross section and a constant applied load, the total deflection of the bar can be determined in terms of P, L, A, and E.
Starting with the one dimensional Hooke’s Law, σ = Eε and substituting P/A for stress and δ/L for strain gives, P/A = E (δ/L) This can be rearranged to give, δ=PL/AE
The product AE is knows as the ____ ____ of the bar.
axial rigidity
If a material is _____ _____, the load and elongation will be proportional.
linear elastic
Uniaxial Deflection (Constant Load, Area and Stiffness);
Provide Elongation Equation for series of bars and explain
If there are a series of bars, then the deflection of each section can be determined and then all deflections summed.
This can be written in equation form as δ total=Σ PiLi/AiEi i
Total Deformation= δ = PL1/A1E1 + PL2/A2E2 + PL3/A3E3
The stiffness (k) and flexibility (f) of a _____ ____ are defined in the same way for a spring. Provide equations
prismatic bar
k = AE/L
f = L/AE
k=stiffness
f=flexibility
A cable is considered an _____ _____ member because it is subjected only to tensile forces
axially loaded
Cables are also known as ______ _____.
wire rope
Cross sectional area of a cable is equal to the cross sectional area of the individual wires, called the ______ ______.
effective area
Under the same tensile load, the elongation of a cable is greater then the elongation of a solid bar of the same material & cross sectional area, because the wire cable _____ ____.
tightens up
The modulus of elasticity of a cable is called the ______ _____, and its less then the modulus of the material of which its made.
effective modulus
The effective modulus of steel cables is about ____ksi, whereas the steel itself has a modulus of about _____ksi.
Wire Cable E= 20,000 ksi
Steel E= 30,000 ksi
When determining the elongation of a cable, the ____ ____ should be used for E, and the ____ ____ should be used for A.
Effective modulus
Effective Area
Supposed for instance that a prismatic bar is loaded by 1 or more axial loads acting at intermediate points along the axis, we can determine the change in length by separating the bar into segments and using this equation_____.
δ total = Σ NiLi/AiEi
Ni is the internal axial force in the segment i.
When solving for the elongation for a prismatic bar that is loaded by 1 or more axial loads acting along the axis, never cut at the _____, only cut at the ____ ______.
Joint
Cross Section
In a statically determinate structure, reactions & internal forces can be determined by a _____-______ _______ & ______ __ ________.
free-body diagram
&
equation of equilibrium
Prove the 3 equations for solving indeterminate structures-
1) Equations of Equilibrium
ΣM = 0
ΣFx = 0
ΣFy = 0
2) Equations of Compatibility
3) Force Displacement Relations
(δ=PL/AE)
Explain the Equations of Compatibility
Equations of Compatibility expresses the fact that the change in length of a bar must be compatible with the conditions at the supports.
Changes in temperature produce expansion, or contraction of structural materials, resulting in ______ ______ & ______ ______.
Thermal Stresses
Thermal Strains
For most structural material, thermal strain (εT) is proportional to the _____ ____. Provide equation α is a property of the material called _____ _____ _____ _____.
Temperature Change
Coefficient of Thermal Expansion
α= Coefficient of Thermal Expansion
ΔT= Change in Temperature
C= Coefficient of thermal expansion
Since strain is a dimensionless quantity, the coefficient of thermal expansion has units equal to the ____ _____ ____ ____.
reciprocal of temperature change
When a sign convention is needed for thermal strains, we usually assume the expansion is ____, and the contraction is ______.
Expansion= Positive
Contraction= Negative
Ordinary structural material expands when _____, and contracts when ______.
heated
cooled
Water is an unusual material from a thermal standpoint. It expands when heated at temperatures above _____ and also expands when cooled below _____. Water has a max density @ ______.
4 degrees celsius
4 degrees celsius
4 degrees celsius
Provide the equation for temperature-displacement relation
δT= εT*L = α*(ΔT)*L δ
T= Temperature elongation
L= Original length
α (alpha)= Coefficient of thermal expansion
(ΔT)= change in temperature
εT= Thermal Strain
The temperature displacement equation can be used to calculate changes in lengths of structural members subjected to uniform _____ _____.
Temperature changes
In structures that have supports that prevent free expansion & contraction, ____ ____, will develop even when the temperature change is uniform throughout the structure.
thermal stress
A ____ ____ ____ with uniform temperature changes will produce thermal strains (and the corresponding changes in Length) without producing any corresponding stresses.
statically determinate structure
A _____ _____ _____ may, or may not develop stresses, depending on the character of the structure and the nature of the temperature change.
statically indeterminate structure
Supposed that a member of a structure is manufactured with its length slightly different from its prescribed length, then the member will not fit into the structure in its intended manner, and the geometry of the structure will be different then planned. Situations such as this are known as ______.
misfits
Sometimes misfits are intentionally created to introduce _____ into the structure at the time it is built. Because these strains exist before _____ are applied to the structure, they are called _______.
strain
loads
pre-strains
Accompanying pre-strains are _______, and the structure is said to be _______.
pre-stresses
pre-stressed
If a structure is _______ ______, small misfits in one or more members will not produce strains or stresses, although there will be departures from the theoretical configuration of the structure.
statically determinate
In a statically determinate structure, misfits react similar to those of a _____ _____.
temperature change
If a structure is _____ ______, the structure in not free to adjust to misfits (Just as it is not free to adjust to certain kinds of _____ _____).
Statically Indeterminate
temperature changes
A simple way to produce a change in length is to tighten a bolt or turnbuckle. In the case of a bolt, each turn will cause the nut to travel along a bolt a distance equal to the spacing ____ of the threads (Called the _____ of the threads).
ρ
pitch
δ = n*ρ
n= number of revolutions
Provide equation for a double-acting turnbuckle
δ = 2n*ρ
n= number of revolutions
