L8 - Multinomial Choice Models Flashcards
(17 cards)
What is different about Multinomial choice models?
The left hand side variable (The choice set) consists of more than two alternatives
- instead of just 0 and 1, it could be the set {1,2,3,4,5} etc
What data do we use in Multinomial choice models?
- Both of these models have more than two outcomes in the dependent variables but their are slight nuances that differentiate them
- Multinomial (Conditional) conditional choice models
-
Nominal scale variable:
- Unique values
- Classification
- No indication of order (e.g. hair colour)
-
Nominal scale variable:
- Ordered Choice models
-
Ordinal scaled data:
- Unique values
- Provide indication of order
- Cannot determine distance between the objects (this makes them different form linear or cardinal variables)
- e.g. in this case cant say 2 is twice a big as 4, just that 4 is greater than 2
- like a satisfaction rating about a product or service
-
Ordinal scaled data:
What is the distribution of the errors term in the Multinomial Logit (MNL) Model?
- we now have more than 1 alternative j
- what do we mean by independently and identically distribution extreme values
- independent –> the error term for alternatives does not give away any information for the error term of another alternative
- identically distributed –> variance of the error term of one alternative is the same of the of another alternatives –> kind of like Homoscedasticity
*

In the MNL model, what is the probability that the decision makers chooses alternative i over all other options?
- So the Utility of alternative i > Utility of alternative j
- assuming that εni is known, then this probability is a cumulative distribution function εnj evaluated at the second formula on the slide
- can multiple across alternatives because we can assume they are independent to one another
- if it isn’t know then we have to integrate the formula see at the end of the slide with respect to each value of εni
- assuming that εni is known, then this probability is a cumulative distribution function εnj evaluated at the second formula on the slide

What does the MNL model probability formula collapse to?
WILL NEED THIS EXPRESS FOR THE EXAM
- This happens because we assume the variance of the error term is equal to π2/6
Denominator is just the numerator added up across all the alternatives
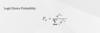
What are the properties of logit probabilities?

What is the maximum likelihood estimator for the MNL model?
- assuming alternatives are independent we can multiple probabilities across alternatives
- However, Non chose alternatives we are raised to the power of 1, so this entire product function collapses to the probability of person n choosing alternative i
- assuming each individual decision making is independent we can further multiple these probabilities across each person in the data set
- log the previous function to make it easier to compute
- set the first-order condition equal to zero to find the maximum likelihood estimator

What can we decompose the probabilities down into?
- Marginal Effects:
- Direct effects
- Cross-effects
- Elasticities:
- Direct elasticities
- Cross-elasticities
What are the marginal effects of probability in Multinomial models?
-
Direct Marginal Effect represents the change in the choice probability of an alternative given a unit change in a variable related to that same alternative
- how does the probability of taking the bus change if a bus ticket increases by £1
-
Cross-Marginal Effect represents the change in the choice probability of an alternative given a unit change in a variable related to a competing alternative.
- how does the probability of taking the bus change if a rail ticket increases by £1
MUST MULTIPLE RESULT BY 100

What are the elasticity effects of probability in Multinomial models?
-
Direct elasticity measures the change in probability of choosing a particular alternative in the choice set with respect to a given percentage change in an attribute of that same alternative.
- how does the probability of taking the bus change if a bus ticket increases by 1%
-
Cross-elasticity measures the change in probability of choosing a particular alternative in the choice set with respect to a given percentage change in an attribute of a competing alternative.
- how does the probability of taking the bus change if a train ticket increases by 1%
TAKE RESULT AS IT COMES (DON’T MULTIPLE BY 100)

What is something special about MNL model with respect to the constants included?
With J alternatives, at most J-1 alternative-specific constants can enter the model, with one of the constants normalised to zero.
- so if you have 4 alternatives, you would include 3 constants in the model –> with one normalised to zero otherwise the model wouldn’t be identified
How is data arranged from MNL models?
- Much include the dependent variables for each alternative for Each individual (separated by colour)
- Hence there are 4 lines for each individual with their own respective explanatory variables

What are the 4 ways in which you can test the ‘fit’ of the model given you have alternative specifications?
- Likelihood Ratio Index
- Can compute this with other specifications as the base to create a comparison
- Pseudo R-squared
- Log-likelihood function (MLE) –> LLmodel
- Log-likelihood function (constant only) –> LLbase
- LL function where you only include the constant(s) of your model

What do the changes in probabilities of the MNL models sum to?
- 0
- This should be for elasticities and marginal effects
How do we deal with the individual decision-makers characteristics in a MNL model?
- e.g. income may be different across participants (cannot estimate coefficient for these variable as differences in these are based across the decision makers)
- How do we deal with them in Multinomial models
- Interact them with the alternative specific constant –> multiple the individual charactistics with alternative specific constants?/ –>multiple income with the constant variable of the different alternatives
- as those with lower incomes would be more sensitive to changes in the costs?
What are the limitations of the (Multinomial) Logit Model?
- Does not accommodation for unobserved “Taste” Variation –>
- People may pick different types of cars –> families would be worried about the size of the car, those on low income may be more interested in the price
- Its fine if we can take these ino account but even then people may still have the exact same income, age, gender, martial status but still have different preferences on the car they want
- MNL might be okay to estimate the average effect but it wont be able to take into account unobserved heterogeneity
- Its fine if we can take these ino account but even then people may still have the exact same income, age, gender, martial status but still have different preferences on the car they want
- People may pick different types of cars –> families would be worried about the size of the car, those on low income may be more interested in the price
- Substitution Patterns
- Model assumes that, given a change in a variable of one altnerative, there would be a equal net effect on the probabilities of ALL OTHER ALTERNATIVES ==> this is quite restrictive as it implies that all other altneratives are equally similiar and dissimiliar which is unrealistic
- Property of Independence from Irrelevant Alternatives (IIA) - the ratio of the choice probabilities of any pair of alternatives is independent of the presence or absence of any other alternative in a choice set.
How is the Indepedence from Irrelevant Alternatives (IIA) property a limitation of Logit models?
- Example: Red-bus Blue-bus problems
- Choice of going to work via Car or Blue bus
- We assume the chance of picking either is 50% or (0.5)
- Therefore the Pc/Pbb = 1
- BUT If we now add a red bus (exactly the same as the blue bus but the colour_
- 33% chance of choosing any option
- Is this realistic given that the red bus and blue bus are identical? –> probably the case the the 50% chance of taking the bulue would be now be split between two buses and the other 50% will still be given to the car
- Problem is that the MN model overestimates the probability of taking either of the buses and underestimates the probability of taking a car
- Is this realistic given that the red bus and blue bus are identical? –> probably the case the the 50% chance of taking the bulue would be now be split between two buses and the other 50% will still be given to the car
- 33% chance of choosing any option



