Hypothesis Testing

Question 1

Hypothesis for 1 Sample Z-Test and 1 Sample T-Test

Answer 1

H_o: µ=μ₀

H_a: µ≠μ₀

Question 2

Hypothesis for Matched Pairs T-Test

Answer 2

H_o: µ_d=0 The mean difference is 0

H_a: µ_d≠0 There is a mean difference

Question 3

Hypothesis for 2 Sample T-Test

Answer 3

H_o: µ₁= µ₂

H_a: µ₁≠ µ₂

Question 4

Hypothesis for 1 Prop Z-Test

Answer 4

H_o: p = p_o

H_a: p ≠ p_o

Question 5

Hypothesis for 2 Prop Z-test

Answer 5

H_o: p₁ = p₂

H_a: p₁ ≠ p₂

Question 6

Conditions for 1 Sample Z-Test

Answer 6

1) sigma (σ)known
2) SRS
3) Normality

Explain normality by the population being normal or by use of CLT

Question 7

Conditons for 1 Sample T-Test

Answer 7

1) sigma (σ) unknown
2) SRS
3) Normality

Explain normality by the population being normal, by use of CLT or by graphing the sample data to show symmetry and no outliers

Question 8

Conditions for Matched Pairs T-Test

Answer 8

1) Two dependent samples
2) sigma (σ) unknown
3) SRS
4) Normality

Explain normality by the population being normal, by use of CLT or by graphing the sample data to show symmetry and no outliers

Question 9

Conditions for 2 Sample T-Test

Answer 9

1) Two independent samples
2) SRS for both samples
3) Normality in both samples

Explain normality by the population being normal, by use of CLT or by graphing the sample data to show symmetry and no outliers

Question 10

Conditions for 1 Prop Z-Test

Answer 10

SRS,

Normality shown by np>10 and n[1-p]>10

Pop at least 10x sample shows that the formula for standard deviation can be used.

Question 11

Conditions for 2 Prop Z-Test

Answer 11

SRS for both samples

Two independent samples,

normality is shown by all 4 parts (n₁p₁>10, n₁[1-p₁]>10, n₂p₂>10, n₂[1-p₂]>10)

Pop at least 10x sample so that the formula for standard deviation may be used

Question 12

1 Sample Z-Test Statistic

Answer 12

Question 13

1 Sample T-Test Statistic

Answer 13

Question 14

2 Prop Z-Test Statistic

Answer 14

Question 15

Matched Pairs T-Test Statistic

Answer 15

Where “mu” = 0

Question 16

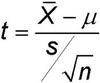
2 Sample T-Test Statistic

Answer 16

Question 17

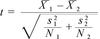
1 Prop Z-Test Statistic

Answer 17

Question 18

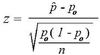
Type 1 Error

Answer 18

Rejecting the null hypothesis when it is actually true

H₀ is true

     H<sub>a</sub>    is true

Reject Ho

**Type I Error**

Correct decision

Accept H₀

Correct Decision

Type II Error

Question 19

Type II Error

Answer 19

Accepting the null hypothesis when the alternative is actually true.

H_o is true

     H<sub>a</sub>    is true

Reject H_o

** **Type I Error

Correct decision

Accept H_o

Correct Decision

Type II Error