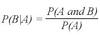All Statistics Flashcards
Center
Mean, Median or Mode
Measures of Spread
How far apart the numbers are in relation to each other
Range, IQR, Variance and Standard Deviation
Shape
Symmetric, normal, skewed left, skewed right, uniform, bimodal
Variability
How spread out numbers in a set are in relation to each other. Measured by spread.
Box Plot
A graph of the 5 number summary
A modified box plot shows if the data set has outliers.
Stemplot
A graph for quantitative data. Each value of the data set is represented by a stem and a leaf. Each leaf may only be 1 digit. Stem plots may have rounded values in place of the actual data.
Histogram
Common distribution for one variable
Dot Plot
A simple graph for small data sets
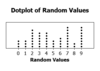
Mean
Average
Median
The middle number in a data set when the numbers are in order.
Sometimes called Q2 or MED
Mode
Most common value within the data
Outliers
A value that doesnt follow the general trend of the data.
Upper limit = Q3 + 1.5(IQR)
Lower limit = Q1 - 1.5(IQR)
Standard Deviation
A measure of spread. The average distance from the mean.
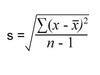
Range
A measure of spread
Maximum-Minimum
5 Number Summary
Used in box plots
Min-Q1-Median-Q3-Max
Individuals
Person/object that is a member of the studied population
Quantitative
Numerical measures (order)
Qualitative
Classification of individuals based on attributes/characteristics (categorical, grouping)
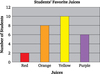
Bar Graph
Used for categorical data
Ogive
A relative cumulative frequency histogram
Pie Chart
Categorical data separated into percentages
Symmetric
Equal on both sides
Minimum
Smallest value within the data
Q3
The median between the median and the maximum
Time Plot
Used to follow trends based on time (connecting)
Q1
Median between the minimum and median
Normal
Perfectly symmetric distribution
Uniform
Histogram with bars of all the same height
Bi-Modal
A graph with 2-peaks
Maximum
Largest value in the data set
Density Curve
On/above horizontal (x) axis; the area underneath is exactly 1
Inflection Points
The point where the graph changes from concave upward to concave downward
Approximately where one standard deviation lies from the mean
68-95-99.7 Rule
Empirical Rule
N(μ, σ)
Short-hand notation for normal distribution
N=Normal
Center=μ (mean)
Spread=σ (standard deviation)
Standard Normal Distribution
Mean=0
Standard Deviation=1
z = (x - μ) / σ
Normal Distribution Equation
Normal Probability Plot
Shows linearity
Explanatory Variable
x, input, independent
Response Variable
y, output, dependent
Scatterplot
Regression Outlier
f
Independent Variable
One event has no effect on the other
Dependent Variable
Two events have effects on eachother
Influential Observation
A point in a scatter plot that changes the regression line
LSRL
Positive Association
As x increases, y increases
As x decreases, y decreases
Positive correlation
Negative Association
As x increases, y decreases
As x decreases, y increases
Negative correlation
Correlation
“r”
As r-value becomes closer to 1, the correlation becomes stronger
Coefficient of Determination
r²
written as a decimal/percentage (% of the change in y is explained by the change in x)
Regression Line
ŷ = a + bx
“line of best fit”
Residual
observed - expected (y-ŷ)
Slope
“b” value in ŷ=a+bx
y-intercept
“a” value in ŷ=a+bx
Residual Plot
A plot representing the x values and residual values (y-ŷ)
Causation
Changes in x cause changes in y
Extrapolation
When you predict for a value outside of the domain
Confounding
effect of y on x, mixed up with effects on y with another variable, z
Common Response
x and y respond to changes in unobserved variables
Lurking Variable
variable that has an important effect on the relationship among variables in the study, but not included
Conditional Distribution
Marginal Distribution
Totals of rows and columns
Observational Study
Does not attempt to influence responses; just observing
Experiment
Deliberately imposes some treatment on individuals in order to observe their response
Population
Entire group of individuals to be studied
Sample
Subset of studied population
Census
Attempting to contact every individual in population
Bias
Systematically favoring certain outcomes
Voluntary Response Sample
A sample from volunteers who are choosing to participate
Convenience Sample
Choosing random participants for a sample convienently instead of stratigically
SRS
Simple Random Sample
Stratified Random Sample
Group(strata) by a common variable, then take SRS of each group (strata)
Table of Random Digits
Used to choose subjects within a sample
Undercoverage
Some group of the population left out in choosing process
Nonresponse
Individual cannot be contacted/does not cooperate
Response Bias
Interviewer may have an influence on respondant’s answers
Experimental Units
Individuals on which an experiment is done
Subjects
Units are people
Placebo Effect
Dummy treatment with no physical effect
Treatment
Specific experimental condition applied to units
Control Group
Group of subjects with no treatment/given a placebo
Statistically Significant
Observed effect is too large to attribute plausibly to chance
Double Blind
Neither subjects/people who have contact with them know which treatment a subject recieves
Block Design
Random assignment of units to treatments is carried out within each block
Matched Pairs
2 treatments:
- match subjects (pairs)
- each subject gets both treatments in random order
(blocking)
Sample Space
Set of all possible outcomes
Probability
Outcome of a random phenomenon is the proportion of times the outcome would occur in a very long series of repetition
Venn Diagram
Probability
Represents probability using area (2+ events)
P(S)=1
Tree Diagram
Probability
Independent
One event does not change the probability of another event
P(S)=1
Area within a venn diagram
P(A&B)=P(A)P(B)
Testing for Independence (Probability)
P(AorB)=P(A)+P(B)-P(A&B)
Disjoint/Mutually Exclusive
Conditional Probability
The probability of A, given B
Complement of an event
(1-p)
Mutually Exclusive/Disjoint
Events cannot occur at the same time
Continuous Random Varibale
Graphed by a density curve (ex. normal curve)
Discrete Random Variable
x has a amount that is countable for possible values
Law of Large Numbers
As sample number increases, the sample results become more accurate
Binomial Distribution
f
Independence
f
binompdf(n,p,k)
n= trials
p= probability of success
k= number of successes
CDF
binomcdf(n, p, k)
n= trials
p= probability success
k= number of successes
What is the shape of the graph?
Skewed Left
What is the shape of the graph?
Skewed Right
Back to Back Stem Plot
Used for comparing two distributions. Leaves are increasing in values away from the stem.
σ2x+y=σ2x+σ2y
Combining variances (population)
μa+bx=a+bμx
property of means
σ2a+bx=bσ2x
property of variances
μx+y=μx+μy
Combining means (population)
σ2x=Σ(Xi- μx)2 Pi
Variance for discrete distribution
μx=ΣXi(Pi)
Mean for discrete distribution
μx=np
Mean of binomial distribution
σ=√np(1-p)
Standard deviation of binomial distribution
Z-Score
The standardized score
z = (x - μ) / σ
B(n,p)
B= binomial distribution
n= sample size (trials)
p= prob of success
Designing Experiments
- Control (Lurking variables)
- Randomization (Treatments)
- Replication
