Hydrodynamik I & II Flashcards
(30 cards)
Definition of a fluid
A fluid deforms continuously, no matter whether the stress is large or small. That means that the constituent parts do not have the same velocity.
Fluids are liquids or gases
What are ideal fluids?
- have no viscosity
- no regards to molecules colliding with each other
Definition of newtonian fluids.
is a fluid in which the viscous stresses arising from its flow, at every point, are linearly correlated to the local strain rate—the rate of change of its deformation over time
Definition of viscosity.
RESISTANCE TO FLOW.
is a measure of its resistance to deformation at a given rate.
- for a liquid - the kinematic viscosity decreases with higher temperature
- for a gas - the kinematic viscosity increases with higher temperature
- it expresses interaction between fluid layers that can transfer momentum between them.
Viscous critical force:
F crit= η^2/ ρ
- if Fs>Fcrit = NICHT visköse Medium –> Turbulente Strömung
- if Fs laminare Strömung
Definition of viscous force bzw. Scherkraft.
fs = −η (v ⋅ A )/d
A: size of the plates
v: speed
d: distane between plates
η : viscosity of the medium
What is the newtons law of viscosity?
–>definition of shear stress, the stress on a surface in y- direction due to flow in x-direction
—> dvx/dy : Shear rate (const= newtonian fluid) it is just a gradient of velocity in a flowing material.
Viscosity = const —> Newtonian fluid
n = f (dVx/dy) –> depends on rate of deformation–> NON newtonian fluid

Explain the diferent plots of shear stress / shear rate, and what meaning do they have to the fluid dynamics.

….
Explain the no slip condition and boundary layer flow in the two plates experiment.
Experiment: two layers and in between a fluid. The upper layer in moving while the other is static. The fluid is moving on the x axis, whereas the shear force is applied in the opposite direction. A flow profile is created, where the smaller the h (distance between the plates) the linear the correspondace.
- the fluid at boundaries move at same velocity as boundary. Meaning: vx (y=0) = 0 ; vx (y=h) = v.
- je näher an der bewegliche Platte, desto schneller die Bewegung der visköse Fluid ist.
- Für ganz kleine h –> lineare Anstieg, also vx (y)= vy/h
Boundary layer:
the distance z = dL when v = 0.99 v . But, dL gets larger with increasing distance from the leading edge of the plate. With increasing thickness of the layer, it becomes unstable which leads to turbulence. This transition is accompanied by a sudden increasing friction and thickness of the boundary layer (dL ≤dT)
*

definition of laminar flow
Laminarefluß ist der parallele Fluss von Partikeln. Es kommt zustande, wenn die Viskosität groß ist und die Strömmung dadurch bestimmt wird.
- The velocity profile resembels a deck of cards. No cross-currents perpendicular to the direction of flow.
- The velocity of flow varies from zero at the walls to a maximum along the cross-sectional centre of the vessel.
- At lower velocities.
- Re > 10^4 transition from laminar –> turbulent flow
- Fs = viskose kritische Kraft =
What is the viscous critical force and what does it measures?
Viscous critical force:
F crit= η^2/ ρ
- if Fs>Fcrit = NICHT visköse Medium –> Turbulente Strömung
- if Fs<fcrit> laminare Strömung</fcrit>
What is the Reynolds number? helps predict flow patterns in different fluid flow situations. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent
The Reynolds number is the ratio of inertial forces to viscous forces within a fluid which is subjected to relative internal movement due to different fluid velocities.
- helps predict flow patterns in different fluid flow situations. At low Reynolds numbers, flows tend to be dominated by laminar (sheet-like) flow, while at high Reynolds numbers flows tend to be turbulent
- aminar flow occurs at low Reynolds numbers, where viscous forces are dominant, and is characterized by smooth, constant fluid motion
Re = ρuL /μ = uL/v
where:
ρ is the density of the fluid (SI units: kg/m3)
u is the flow speed (m/s)
L is a characteristic linear dimension (m)
μ is the dynamic viscosity of the fluid (Pa·s or N·s/m2 or kg/(m·s))
v is the kinematic viscosity of the fluid (m2/s)
Relation between Re , F crit, & laminar/turbulent flow.
- Re small = laminar flow –> Fs < Fcrit => viscous medium
- Re big = turbulent flow –> Fs > Fcrit => not viscous medium
–> Pt : point of transition from laminar to turbulent flow mit zunehmender Länge und Geschwindigkeit. ( Re= 10^4 = 2000)
define kinematic viscosity.

define shear strain

Explain Stockes Law
in a falling sphere viscosimeter;

Wann stoppt ein Bakterium, wenn es aufhört aktiv zu schwimmen?

What distance is it E. coli still swimming after it stops beating the flagellum?

How much POWER is needed to push a bacteria forward?

Erklären Sie den Fluss durch Kapillaren als Fluss durch Konzentrichen Röhren dargestellt wird.
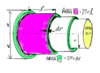
–> The inner cyclinders move faster than the outer ones
- the central cylinder has a driving force. F= π* r^2 * pressure difference.
- there is also a frictional force, Ff= (2πrl)*η* (-dv / dr) , the laste term is the shear rate. => Ff changes with the radius
- Fd = Ff at steady movement => π* r^2 * pressure difference = (2πrl)*η* (-dv / dr)
- Through integration–> velocity profile. v(r) = - (dif. p/ 2πlη) * (1/2*r^2 +C)
- At no slip condition: r= R & v(r) =0 –> goes to zero.
- v(r) = - (dif. p/ 2πlη) * (R^2 -r^2) => PARABOLIC FUNTION
=> vmax is at the center, where r=0, and the flow has the largest distance from the surface.

What is volume flow (Jv) and what is its relation with the Hagen-Poiseuille equation?
Beschriebt die laminare Strömung eines homogenen Newtonsche Fluids durch ein Rohr in abhängigkeit von Eigenschaften vom Fluid und Rohr.
- incompressible fluids
- laminar flow
–> Blood flow!
- der Fluss in den Kapillaren hängt von der 4te Potenz von R ab
- Bei einer Innendurchmesser Verdopplung –> hohen Fluss bzw. hohen Druck
- pressure increase –> Jv will increase
- if the viscosity of blood increases –> Jv will decrease

Explain the following Begriffe and its consequeances in fluid dynamics.
- Arteriosclerosis
- Stenosis
- Aneuryms
- Arteriosclerosis: Thickening of the walls of the arteries and more rigidyty in them. –> for the same flow the blood pressure must increase
- Stenosis: narrowing of the arteries –> in arties radius are decreased so is the volume flow rate, which leads to low blood pressure.
- Aneurym: blowing out of the arteries, wall thickness –> turbulent flow
Properties of blood in fluid dynamics
- non- newtonian fluid, which means that the viscosity represents a function of the shear rate or of the dv/dh. (fluid)
- Viscosity is reduced at higher flow pressure
- The increase of η at low flow speed is caused by aggregation of the erythrocytes into rouleaux (“Geldrollenbildung”)
- Viscosity increases with the haematocrit, 50% more –>2*η
- Blood Cells are strongly deformed in narrow capillaries.
- In large vessels the RBCs concentrate in the centre of the vessel, where the shear is minimal => flattering og the flow parabola
- Capillary diameter is not constant and the velocity profile is only slowly adapting.
- Pressure of blood is PULSED. –> partially compensated by elastic blood vessels.
- VISCOELASTIC ( due to RBCs), η alters as a function of time after a change in stress.
- Pulse speed: function of DENSITY (ρ) not viscosity. –> Moens-Kortevef equation
- Branching points are critical for maintaining laminar flow.
- low bifurcation angles - laminar flow, bigger angles turbulence.
- The Pt bzw. critical Re. depends on the angle α , Re higher for a high angle.
What is the Farheus-Lindqvist Effect?
describes how the viscosity of a fluid, in this case blood, changes with the diameter of the tube it travels through. In particular there is a ‘decrease in viscosity as the tube’s diameter decreases
–>This is because erythrocytes move over to the centre of the vessel, leaving only plasma near the wall of the vessel.
How does a sudden narrowing of a vessel affects the velocity profile?
–> narrowing of the parabolic profile in order to maintain laminar flow