Geometry Ch 7 - Similarity Flashcards
(21 cards)
Ratio
Comparison of two quantities. You can write the ration of a to b or a : b as the quotent a/b when b ≠ 0
Proportion
A statement that two ratios are equal.
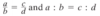
Extended Proportion
When three or more ratios are equal.
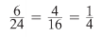
Properties of Proportions

Cross-Product Property
The product of the extremes is equal to the product of the means.

Scale Drawing
A drawing that shows a real object with accurate sizes reduced or enlarged by a certain amount (called the scale). The scale is shown as the length in the drawing, then a colon (“:”), then the matching length on the real thing.
eg. 1 in = 10 ft
Similar Polygons
Have corresponding angles that are congruent and corresponding sides that are proportional.
Similarity Ratio
The ratio of the lengths of corresponding sides.
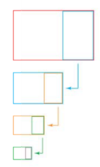
Golden Rectangle
A rectangle that can be divided into a square and a rectangle that is similar to the original rectangle.
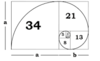
Golden Ratio
A special number found by dividing a line into two parts so that the longer part divided by the smaller part is also equal to the whole length divided by the longer part. It is often symbolized using phi ( Φ, φ ), after the 21st letter of the Greek alphabet. … Phi is usually rounded off to 1.618.
Angle-Angle Similarity (AA ∼) Postulate
If two angles of one triangle are congruent tot two angles of another triangle, then the triangles are similar.

Side-Angle-Side Similarity (SAS ∼) Theorem
If an angle of one triangle is congruent to an angle of a second triangle, and the sides including the two angles are proportional, then the triangles are similar.
Side-Side-Side Similarity (SSS ∼) Theorem
If the corresponding sides of two triangles are proportional, then the triangles are similar.
Indirect Measurement
Using similar triangles and measurements to find distances that are difficult to measure directly.
The altitude to the hypotenuse of a right triangle…
… divides the triangle into two triangles that are similar to the original triangle and to each other.
Geometric Mean
The central number in a geometric progression (e.g., 9 in 3, 9, 27 ), also calculable as the n th root of a product of n numbers. For any two positive numbers a and b, the geometric mean of a and b is the positive number x such that a/x = x/b. This means that x = √ab.
The length of the altitude to the hypotenuse of a right triangle…
…is the mean of the lengths of the segments of the hypotenuse.
The altitude to the hypotenuse of a right triangle separates the hypotenuse so tha…
… the length of each leg of the triangle is the geometric mean of the length of the adjacent hypotenuse segment and the length of the hypotenuse.
Side-Splitter Theorem
If a line is parallel to one side of a triangle and intersects the other two sides, then it divides those two sides proportionally.
Corollary to Side-Splitter Theorem
If three parallel lines intersect two transversals, then the segments intercepted on the transversals are proportional.

Triangle-Angle-Bisector Theorem
If a ray bisects an angle of a triangle, then it divides the opposite side into two segments that are proportional to the other two sides of the triangle.


