Geometry Ch 3 - Parallel and Perpendicular Lines Flashcards
What is a Transversal?
A line that intersects two coplanar lines at two distinct points.
Example: The diagram shows the eight angles formed by a transveral t and two lines l and m.
What are Alternate Interior Angles?
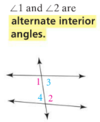
What are Same Side Interior Angles?
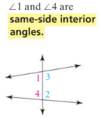
What are Corresponding Angles?
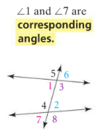
What is the Corresponding Angles Postulate?
What is the Alternate Interior Angles Theorem?
What is the Same-Side Interior Angles Theorem?
What is the Alternate Exterior Angles Theorem?
What is the Same-Side Exterior Angles Theorem?
What is the Converse of the Corresponding Angles Postulate?
What is the Converse of the Alternate Interior Angles Theorem?
What is the Converse of the Same-Side Interior Angles Theorem?
What is the Converse of the Alternate Exterior Angles Theorem?
If two lines are parallel to the same line, then…
they are parallel to each other.
In a plane, if two lines are perpendicular to the same line, then…
they are perpendicular to each other.
What is the Triangle Angle-Sum Theorem?
The sum of the measures of the angles of a triangle is 180.
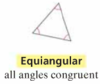
What is an Equiangular Triangle?
A triangle with all angles congruent.
What is an Acute Triangle?
A triangle with all angles acute.
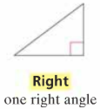
What is a Right Triangle?
A triangle with one right angle.
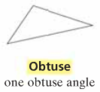
What is an Obtuse Triangle?
A triangle with one obtuse angle.
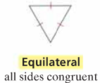
What is an Equilateral Triangle?
A triangle with all sides congruent.
What is an Isosceles Triangle?
A triangle with at least two sides congruent.
What is a Scalene Triangle?
A triangle with no sides congruent.
What is the Exterior and Interior Angles of a Polygon?
What is the Triangle Exterior Angle Theorem?
What is a Great Circle?
The intersection of a sphere and a plane that contains the center of the sphere.
What is Euclid’s Parallel Postulate?
Through a point not on a line, there is one and only one line parallel to the given line.
What is the Spherical Parallel Postulate?
Through a point not on a line, there is no line parallel to the given line.
What is a Polygon?
A closed plane figure with at least three sides that are segments. The sides intersect only at their endpoints, and no adjacent sides are collinear.
What is a Convex Polygon?
A polygon having no diagonal with points outside the polygon.
What is a Concave Polygon?
A polygon having at least one diagonal with points outside the polygon.
What is the Polygon Angle-Sum Theorem?
The sum of the measures of the angles of an n-gon is (n - 2)180.
Note: By dividing a polygon with n sides into n - 2 triangles, you can show that the sume of the measures of the angles of any polygon is a multiple of 180.
What is the Polygon Exterior Angle-Sum Theorem?
The sum of the measures of the exterior angles of a polygon, one at each vertex, is 360.
What is an Equilateral Polygon?
A polygon having all sides congruent.
What is an Equiangular Polygon?
A polygon having all angles congruent.
What is a Regular Polygon?
A polygon that is both equilateral and equiangular.
What is the Slope of a line?
The ratio of the vertical change (rise) to the horizontal change (run) between any two points (x1, y1) and (x2, y2) of the line.
Equation: Slope = Vertcal Change / Horizontal Change = rise / run = (y2 - y1) / (x2 - x1)
The slope of a line indicates the steepness of the line and whether it rises or falls from left to right.
What is the Slope-Intercept Form of a linear equation?
y = mx + b, where m is the slope of the line, and b is the y-intercept.
What is the Standard Form of Linear Equation?
Ax + By = C, where A, B and C are real numbers, A and B are not both zero.
Note: To graph an equation written in standard form, you can readily find two points for the graph by finding the x- and y-intercepts. See example.
How do you convert a linear equation from Standard to Slope Intercept form?
Solve for y
What is the Point-Slope Form for a Linear Equation?
For a nonvertical line through point (x1, y1) with slope m; y - y1 = m(x - x1)
