Geometry Ch 11 - Surface Area and Volume

Question 1

Polyhedron

Answer 1

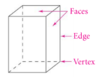
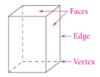
A three-dimensional figure whose surfaces are polygons. Each polygon is a face of the polyhedron. An edge is a segment that is formed by the intersection of two faces. A vertex is a point where three or more edges intersect.

Question 2

Euler’s Formula

Answer 2

The numbers of faces (F), vertices (V), and edges (E) of a poolyhedron are related by the formula F + V = E + 2

Question 3

Cross Section of a Solid

Answer 3

The intersection of a solid and a plane.

Note: You can think of it as a very thin slice of a the solid.

Question 4

Literal Equation

Answer 4

An equation involving two or more variables.

Question 5

Prism

Answer 5

A polyhedron with exactly two congruent, parallel faces, called bases. Other faces are lateral faces. You name it by the shape of its bases.

A prism may either be right or oblique.

Question 6

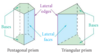
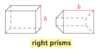
Right Prisms

Answer 6

The lateral faces are rectangles and a lateral edge is an altitude.

Question 7

Oblique Prism

Answer 7

A prism with bases that are not aligned one directly above the other. The lateral faces are parallelograms.

Question 8

Lateral Area of a Prism

Answer 8

The sum of the areas of the lateral faces.

Question 9

Surface Area of a Prism

Answer 9

The sum of the lateral area and the area of the two bases.

Question 10

Lateral and Surface Areas of a Prism

Answer 10

Question 11

Cylinder

Answer 11

A solid geometric figure with straight parallel sides and a circular or oval cross section. It has two congruent bases that are circles.

Question 12

Altitude of a Cylinder

Answer 12

A perpendicular segment that joins the planes of the bases. It is the height of a cylinder.

Question 13

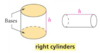
Right Cylinders

Answer 13

A cylinder with the bases circular and with the axis joining the two centers of the bases perpendicular to the planes of the two bases.

Question 14

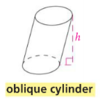
Oblique Cylinder

Answer 14

A cylinder that ‘leans over’ - where the sides are not perpendicular to the bases.

Question 15

Lateral and Surface Areas of a Cylinder

Answer 15

The rectangle resulting from “unrolling” the curved surface of a cylinder. The surface are of a right cylinder is the sume of the lateral area and the areas of the two bases.

Lateral Area = 2πrh = πdh

Surface Area = Lateral Area + 2B = 2πrh + 2πr²

Question 16

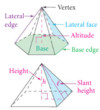
Pyramid

Answer 16

A polyhedron in which one face (the base) can be any polygon and the other faces (the lateral faces) are triangles that meet at a common vertex (called the vertex of the pyramid). You can name it by the shape of its base. The altitude is the perpedicular segment from the vertex to the plane of the base. the length of the altitude is the height h of the pyramid.

Question 17

Regular Pyramid

Answer 17

A pyramid whoe base is a regular polygon and whose lateral faces are congruent isosceles triangles.

Question 18

Slant Height of a Pyramid

Answer 18

The length of the altitude of a lateral face of the pyramid.

Question 19

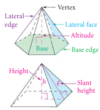
Lateral area of a pyramid…

Answer 19

The sum of the areas of the congruent lateral faces.

Note: You can find the formula for the lateral area of a pyramid by looking at its net.

Question 20

Lateral and Surface Areas of a Regular Pyramid

Answer 20

Question 21

Cone

Answer 21

It’s “pointed” like a pyramid, but its base is a circle.

Question 22

Lateral and Surface Areas of a Cone

Answer 22

Question 23

Volume

Answer 23

The space a figure occupies. It is measured in cubic units such as cubic inches (in³), cubic feet (ft³), etc…

Question 24

Cavalieri’s Principle

Answer 24

If two space figures have the same height and the same cross-sectional area at every level, then they have the same volume.

Question 25

Volume of a Prism

Answer 25

The volume of a prism is the product of the area of a base and the height of the prism.

V = Bh

Question 26

Volume of a Cylinder

Answer 26

The product of the area of the base and the height of the cylinder.

V = Bh = πr²h

Question 27

Composite Space Figure

Answer 27

Three-dimensional figure that is the combination of two or more simpler figures. You can find the volume by adding the volumes of the figures that are combined.

Question 28

Volumes of a Pyramid

Answer 28

The volume of a pyramid is one third the product of the area of the base and the height of the pyramid.

V = 1/3(Bh)

Because of Cavalieri’s Principle, the volume formula is true for all pyramids, including oblique pyramids. The height h of an oblique pyramid is the length of the perpendicular segment from the vertex to the plane of the base.

Question 29

Volume of a Cone

Answer 29

The volume of a cone is one third the product of the area of the base and the height of the cone.

V = 1/3(Bh) = 1/3(πr²h)

Question 30

Sphere

Answer 30

The set of all points in space equidistant from a given point called the center.

Question 31

Surface Area of a Sphere

Answer 31

The surface area of a sphere is four times the product of π and the square of the radius of the sphere.

Surface Area = 4πr²

Question 32

Volume of a Sphere

Answer 32

The volume of a sphere is four thirds the product of π and the cube of the radius of the sphere.

V = 4/3(πr³)

Question 33

Similar Solids

Answer 33

Have the same shape, and all their corresponding dimensions are proportional. The ratio of corresponding linear dimensions of two similar solids is the similarity ratio. Any two cubes are similar, as are any two spheres.

Question 34

Areas and Volumes of Similar Solids

Answer 34

If the similarity ratio of two similar solids is a : b then

(1) the ratio of their corresponding areas is a² : b², and
(2) the ratio of their volumes is a³ : b³