Funktionen

Question 1

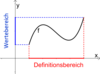
What is a function’s Definitionsmenge?

Answer 1

All of the possible x-values the function could have.

Question 2

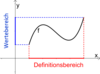
What is a function’s Wertmenge?

Answer 2

All of the possible y-values a function could have.

Question 3

How can you show that a graph is a function?

Answer 3

You use the vertical line test. That means, you imagine drawing all possible vertical lines on the graph. If any vertical line would intersect the function more than once, it’s not a function.

Question 4

How do you shift f(x)=x² to the right by h?

Answer 4

You put a “-h” in with the x term.

g(x)=(x-h)²

Question 5

How do you shift f(x)=x² to the up by k?

Answer 5

You put a “+k” at the end.

g(x)=x²+k

Question 6

How do you mirror f(x)=x²+k vertically (over the x-axis)?

Answer 6

You multiply the whole function by -1.

g(x)= -(x²+k).

Question 7

How do you mirror f(x)=x²+k horizontally (over the y-axis)?

Answer 7

You multiply the x-part by -1.

g(x)=(-x)²+k.

Question 8

How do you vertically stretch f(x)=x²+k by a?

Answer 8

You multiply the whole function by a.

g(x)=a(x²+k).

Question 9

How do you horizontally stretch f(x)=x²+k by scale factor b?

Answer 9

You multiply the whole x-part by 1/b.

g(x)=(1/b x)²+k.

Question 16

Where is the vertex and line of symmetry for

f(x)=a(b(x-h)²+k)?

Answer 16

Vertex: (h, a•k)

Line of symmetry: x=h