Functions HL

Question 1

What are the three ways to solve a quadratic equation?

Answer 1

• Factorization
• Completing the square
• The quadratic formula

Question 2

What are the steps to solving a quadratic equation by factorising?

Answer 2

1. Get everything on one side, leaving just 0 on the other. (i.e. x²-2x+1=0).
2. Factorise, so you get something like (x+a)(x+b)=0.
3. Solve each parenthesis for x. (i.e. x+a=0 and x+b=0)

Question 3

How can you recognize that an equation is quadratic?

Answer 3

Some variable is squared.

It can always be written as:

ax²+bx+c=0

Question 4

What are the steps for factorising a quadratic equation?

ax²+bx+c=0

Answer 4

1. Factor out any common factors. (So anything that goes into all of the terms. i.e. 6x²-2x-8 = 2 (3x²-x-4))
2. Make a list of all the factors that multiply to make ac.
3. Check to see which two factors from step two add to the b term.
4. Rewrite the equation, separating the middle term into the two factors you found.
5. Take the common factors out of the first two terms and the last two, and regroup.

For example, 3x²-x-4:

1. 6x²-2x+8=2(3x²-x-4). Now I need to factorise 3x²-x-4
2. 3•-4=-12, so the factors are 1•-12, -1•12, 2•-6, -2•6, 3•-4, -3•4
3. Do any of the pairs add to -1? Yep, 3+-4=-1.
4. 3x²+3x-4x-4
5. 3x(x+1) - 4(x+1) = (3x-4)(x+1). So the answer is 6x²-2x+8=2(3x-4)(x+1).

Question 5

What does the graph of f(x)=x² look like? What are the vertex and line of symmetry?

Answer 5

Vertex: (0,0)

Line of symmetry: x=0

Question 7

How can you find the root if a quadratic equation has “two equal real roots”?

Answer 7

This means the discriminant is zero, so your solution is just

Question 8

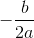
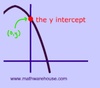
How do you find the y-intercept of ANY function?

Answer 8

You plug in 0 for x and solve for y….because when you’re on the y-axis, the x-coordinate MUST be equal to 0.

Question 9

How do you find the x-intercept of ANY function?

Answer 9

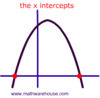
You plug in 0 for y and solve for x….because when you’re on the x-axis, the y-coordinate MUST be equal to 0.

Question 10

Where is the vertex and line of symmetry for

f(x)=a(b(x-h)²+k)?

Answer 10

Vertex: (h, a•k)

Line of symmetry: x=h

Question 14

How do you know when there are two repeated real roots for ax²+bx+c?

Answer 14

You find when the discriminant is 0.

So solve b²-4ac=0.

Question 15

How do you know when there are no real roots for ax²+bx+c?

Answer 15

You find when the discriminant less than 0.

So solve b²-4ac<0.

Question 16

How do you know when there are two real roots for ax²+bx+c?

Answer 16

You find when the discriminant greater than 0.

So solve b²-4ac>0.

Question 17

When you need to use the “complete the square” method?

Answer 17

Whenever you need the form of the equation to tell you the vertex.

f(x)=(x-h)²+k

Question 18

What’s the quadratic formula?

Answer 18

Question 19

How do you turn

f(x)=ax²+bx+c

into the “vertex” form

f(x)=a(x-h)²+k?

Answer 19

Question 20

What is a coefficient?

Answer 20

A coefficient is a number that is multiplying (it is attached to) a variable, like an x or any other letter.

e.g.

3x² + 2x - 4

3 is the coefficient of x²,

and 2 is the coefficient of x.

Question 21

What is the leading coefficient?

Answer 21

The leading coefficient, is the number that is attached to the x with the highest power.

e.g. in the trinomial

4x² + 3x + 9

the leading coefficinent is 4

Question 22

What is a constant?

Answer 22

A constant is a number that is not attached to a variable (like an x, or any other number).

e.g. 3x² + 4x + 7

7 is the constant.

3 and 4 are coefficients.

3 is the leading coefficient.

Question 23

What is a quadratic?

Answer 23

The general quadratic looks like:

ax² + bx + c

“Quad” means “square”, which in math means to the power of 2. So a quadratic is an equation that contains an x², and this is the highest power. There can’t be, for example x³, nor x⁴, and so on. Only the square is the highest power. Quadratic expression contains three terms, which makes it a trinomial.

Question 24

What is a function’s domain? (i.e., “what does domain mean?”)

Answer 24

Domain is “all of the possible x-values” that a relation has. You can think of it as all the numbers you could put into the function machine.

Question 25

What is a function’s range (i.e., what does range mean for functions?)

Answer 25

Range is “all of the possible y-values” that come out of a relation.

Question 26

How can you show that a graph is a function?

Answer 26

You use the vertical line test. That means, you imagine drawing all possible vertical lines on the graph. If any vertical line would intersect the function more than once, it’s not a function.

Question 27

What does this mean?

Answer 27

It can also be written as f(g(x)). This means you put the whole g(x) function inside the brackets of “f”. Then you use this as the argument for the “f” function.

Question 31

How can you tell if a function has an inverse just by looking at the graph?

Answer 31

You use the horizontal line test. That means, you imagine drawing all possible horizontal lines on the graph. If any horizontal line would intersect the function more than once, there is no inverse.

(That’s ‘cause when you swap the x and y, this morphs into the vertical line test for functions.)

Question 33

Where is the vertex and line of symmetry for

f(x)=a(b(x-h)²)+k?

Answer 33

Vertex: (h, k)

Line of symmetry: x=h

Question 34

How do you have to change the function “f(x)” if you want to shift it horizontally? (For example, to the right by 3 or by the left by 3.)

Answer 34

You put a “-h” in with the x term.

f(x)=2^x

g(x)=f(x+3)=2^x+3

h(x)=f(x-3)=2^x-3

Question 35

How do you have to change the function “f(x)” if you want to shift it vertically? (For example, up or down by 3.)

Answer 35

You put a “+k” at the end.

f(x)=2^x

g(x)=f(x)+3=2^x+3

h(x)=f(x)-3=2^x-3

Question 36

How do you have to change the function “f(x)” if you want to reflect it in the x-axis (aka “vertically”)?

Answer 36

You multiply the whole function by -1.

The new function is -f(x).

Question 37

How do you have to change the function “f(x)” if you want to reflect it in the y-axis (aka “horizontally”)?

Answer 37

You multiply the x-part by -1.

The new function is f(-x).

Question 38

How do you have to change the function “f(x)” if you want to stretch it vertically by a scale factor “a”?

Answer 38

You multiply the whole function by a.

If a is bigger than 1, it’s going to stretch the function so that it’s taller.

If a is smaller than 1, it’s going to compress the function so that it’s shorter.

Question 39

How do you have to change the function “f(x)” if you want to stretch it horizontally by a scale factor of “b”?

Answer 39

You multiply the whole x-part by 1/b. (Be careful that you first factor b out of a horizontal shift, if necessary.)

Question 40

What is an inverse function?

Answer 40

It’s denoted with a ^-1 exponent after the function letter. And it basically undoes a function. So if f(3)=5, this means we put in 3 and we get out 5. Therefore, f^-1(5)=3. We put 5 into the inverse and get out 3. It’s exactly the reverse of the original function–it literally swaps the roles of x and y.

Question 41

How would you describe the transformation from P(t) to Q(t)?

Answer 41

This is a vertical stretch with a scale factor of 2. (Notice that each point of Q is twice as far from the axis as P.)

So Q(t)=2P(t)

Question 42

How would you describe the transformation from P(t) to R(t)?

Answer 42

This is a horizontal stretch with a scale factor of 1/2. (Notice that each point of R is half as far from the axis as P.)

So R(t)=P(2t)

Question 43

What type of transformation does the following function represent?

f(x)=(x-2)²+2

Answer 43

It translates the x² function to the right by 2 and up by 2.

Question 44

How is the domain and range of a function related to the domain and range of the inverse?

Answer 44

• The domain of the original function is the range of the inverse.
• The range of the original function is the domain of the inverse.

(Because all of the xs and ys swap in the inverse.)

Question 45

How do you find the inverse, f^-1(x), of the function f(x) algebraically?

Answer 45

1. Write down f(x), but use the letter “y” rather than “f(x)”.
2. Swap the “x” and “y” letters.
3. Rearrange the equation so the “y” is alone.
4. Low key replace the “y” with “f^-1(x)” and pretend you never turned it into a y in the first place.

Question 47

How do you sketch the inverse of a function?

Answer 47

The inverse is a reflection of the original function over the line y=x. The easiest way to sketch it is to:

1. Choose a point on the original function. For example: (1,2).
2. Swap the values to get the matching point on the inverse function. For example: (2,1).
3. Repeat this process for a couple of points and or any asymptotes.
4. Connect the dots, trying to match the general shape of the original function. In the end, it should look like a mirror image of the original function over the diagonal line y=x.

Question 55

If I have a point A(x,y) on my function f, where is the image of that point, A’, on the inverse function, f^–1?

Answer 55

The inverse literally swaps the x and y values.

So if A is (1, 4), then A’ is (4, 1).

Question 56

What is the equation for the sum of all roots of a polynomial?

Answer 56

Question 57

What is the equation for the product of all roots of a polynomial?

Answer 57

Question 58

Given this graph of a 4th degree polynomial, how many real roots and complex roots are there? What are the real roots?

How can you use this graph to find the equation of the function.

Answer 58

There are 2 real roots: x=-4 and x=2

Since the degree is “4”, there must then be 2 complex roots, since there must be 4 total roots.

The equation of the graph would be f(x)=(x+4)(x-2)(ax^2+bx+c). To find a,b,c, I would need to plug in (0,-32) and another point and solve the system of equations.