Functions (AA SL) Flashcards
(15 cards)
What is a function’s domain? (i.e., “what does domain mean?”)
Domain is “all of the possible x-values” that a relation has. You can think of it as all the numbers you could put into the function machine.
- On a graph, you simply look for the furthest left point and the furthers right point and put them in an inequality.
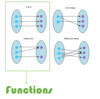
- In a mapping, the domain is the left-hand oval.

What is a function’s range (i.e., what does range mean for functions?)
Range is “all of the possible y-values” that come out of a relation.
- On a graph, you simply look for the lowest point and highest point on the graph and put them in an inequality.
- In a mapping, the domain is the right-hand oval.

How can you show that a graph is a function?
You use the vertical line test. That means, you imagine drawing all possible vertical lines on the graph. If any vertical line would intersect the function more than once, it’s not a function.

How do you show a relation mapping is a function?
Any relation that is “to 1” is a function.
What does “image” mean when talking about functions?
For example, find the image of x =2 for the function y=x+1.
The image of a function is the set of all outputs of the function. So remember that these words are the same (for your purposes).
- output
- range
- y-value
- image
In the example, it wants you to substitute 2 for x into the function.
y=2+1=3
The image is y=3
What does this mean?

It can also be written as f(g(x)). This means you put the whole g(x) function inside the brackets of “f”. Then you use this as the argument for the “f” function.
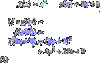
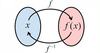
What is an inverse function?
- It’s denoted with a -1 exponent after the function letter.
- It basically undoes a function.
So if f(3)=5, this means we put in 3 and we get out 5. Therefore, f-1(5)=3. We put 5 into the inverse and get out 3. - It’s exactly the reverse of the original function–it literally swaps the roles of x and y.
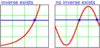
How can you tell if a function has an inverse just by looking at the graph?
You use the horizontal line test. That means, you imagine drawing all possible horizontal lines on the graph. If any horizontal line would intersect the function more than once, there is no inverse.
(That’s ‘cause when you swap the x and y, this morphs into the vertical line test for functions.)
How can you tell if a function has an inverse just by looking at the mapping?
Only 1-to-1 functions have an inverse.
How is the domain and range of a function related to the domain and range of the inverse?
- The domain of the original function is the range of the inverse.
- The range of the original function is the domain of the inverse.
(Because all of the xs and ys swap in the inverse.)

How do you find the inverse, f-1(x), of the function f(x) algebraically?
- Write down f(x), but use the letter “y” rather than “f(x)”.
- Swap the “x” and “y” letters.
- Rearrange the equation so the “y” is alone.
- Low key replace the “y” with “f-1(x)” and pretend you never turned it into a y in the first place.
How do you sketch the inverse of a function?
The inverse is a reflection of the original function over the line y=x. The easiest way to sketch it is to:
- Choose a point on the original function. For example: (1,2).
- Swap the values to get the matching point on the inverse function. For example: (2,1).
- Repeat this process for a couple of points and or any asymptotes.
- Connect the dots, trying to match the general shape of the original function. In the end, it should look like a mirror image of the original function over the diagonal line y=x.

Where is the vertex and line of symmetry for
f(x)=a(b(x-h)2)+k?

Vertex: (h, k)
Line of symmetry: x=h

If I have a point A(x,y) on my function f, where is the image of that point, A’, on the inverse function, f–1?
The inverse literally swaps the x and y values.
So if A is (1, 4), then A’ is (4, 1).
What are you supposed to do when you see the instruction “Evaluate”?

You’re supposed to plug that number into the function. Find out what the output of the function is for that input.



