Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

Comp 2280 Comp Sys > Finals > Flashcards

Finals Flashcards

1
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Provide the symbol table for the following:

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

What are the three types of number encoding?

A
  1. Sign Magnitude Representation
  2. 1’s complement representation
  3. 2’s complement representation
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

How is a Sign Magnitude Representation encoded?

What makes this encoding ackward?

Encode: -+10 (using 8 bits)

Encode: -+7 (using 4 bits)

Encode: +-123

A
  • Use MSB to represent the sign of the number (0 for +, 1 for - )
  • Use remaining n-1 bits for the magnitude (that is the absolute value) of the number
  • The magnitude is encoded using unsigned number encoding
  • +-10 = 10001010 (for neg), 00001010 (for pos)
  • +-7 = 1111(for neg), 0111(for pos)
  • -+123 = 11111011(for neg), 01111011(for pos)
  • Ackward because:
    • There are two distinct representations for value 0, 0000 and 1000
    • Arithmetic
      • If signs are different we need to
        • determine the number with the larger magnitude
        • Subtract the larger magnitude number by the smaller
        • adjust sign as necessary
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

What is the one’s complement representation?

  • Encode +-5 (using 4 bits)
  • +-101 (using 8 bits)

What makes this encoding ackward?

Using n = bits, represent 0 as 11111111 and compute, 0+1

A
  • Positive numbers have MSB 0, and the same encoding for unsigned numbers.
  • Negative numbers are encoded as the bit-wise negation of the representation of the numbers absolute value
  • Encodings:
    • +-5 = 0101 (for pos), 1010(for neg)
    • +-101(8 bits) =01100101(for pos), 10011010(for neg)
  • Ackward
    • two distinct 0’s, 0000, 1111
    • drawbacks with arithmetic
      • 11111111 (neg 0) + 1 = 000000000
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

What is two’s complement encoding?

Encode:

  • +-12 (using 8 bits)
A
  • Non-negative numbers have 0 in MSB and encoded using unsigned number encoding
  • Negative numbers uses the “two’s complement” of the representation of the number’s absolute value
    • you toggle every bit and then add 1 to the result.
    • self-inverting, apply twice and you get back your original number
    • As a consequence MSB sign bit, 0 for non-neg, 1 for neg
  • Encodings:
    • +-12 = 00001100 (for pos), 11110100(for neg)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

What are the advantages to two’s complement representation?

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Draw the timing diagram of the following:

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

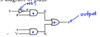
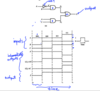
Provide the timing diagram for the following circuit:

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

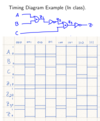
When running a subroutine, jumping is handled by the PC register value.

When about to jump, the PC register value is saved for the return.

Where is that value saved?

A

The PC’s value is saved in R7

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

LC-3 ISA provides two basic instructions for updating the PC register for subroutines?

What are they/

A

JSR and RET

JSR

  • The instruction saves the content of the PC register to R7 and jumps to the address specified by the label in the instrucitons
    • PC holds the address of the instruction following the instruction being executed.

RET

  • Causes the return from the subroutine to the caller
  • It loads the content of R7 into PC
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

Provide a simple example code of using a subroutine.

A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

JSR is limited to a jump of -210 to 210-1

How would you jump further than that?

A

JSSR

Put the address of the start of the subroutine into a register (LEA R5, mySub)

Call subroutine using JSSR specifying the register that holds the address to the subroutine (JSRR R5)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

In order to use the RTS what concepts do we need?

A
  • A stack pointer - a register that holds the address of the top of the runtime stack (TOS)
  • Push/pop operations - these allow you to push and pop items onto the RTS
  • A frame pointer - this is used to allow you to work with teh current activation record.
  • An activation record (for a subroutine call) is the space allocated on the RTS for arguments and return value(s) for the subroutine call.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

What register does LC-3 us for the Stack Pointer and the Frame Pointer?

A

R6 = Stack Pointer (SP)

R5 = Frame Pointer

17
Q

What is the code to initialize the stack?

A

.orig x3000

LD R6, STACKBASE

…

…

STACKBASE .FILL 0x4000

18
Q

What is the code to push Rx onto a stack?

A

ADD R6,R6,#-1 //allocate space at the top of the stack

STR Rx,R6,#0 //store Rx in that new space provided

19
Q

What is the code to pop the content at the top of thee RealTime Stack into register Rx?

A

LDR Rx, R6,#0 //get the item from the top

ADD R6,R6,#1 //reduce the top of the stack

20
Q

What is the basic idea for using registers in subroutines?

A
  1. Push each register you intend on using onto the stack at the start of the subroutine
  2. Use the registers as needed in the subroutine
  3. Before the call to RET, pop the registers in the reverse order that they were pused on the stack
21
Q

Provide the basic code to:

  • Initialize stack
  • Jump to a subroutine
  • Save the registers (R1,R2) to a stack
  • return the registers (R1,R2) from the stack
  • Return back to main call
A
22
Q

What is the value of R6 for lines:

  1. 3
  2. 12
  3. 15
  4. 24
  5. 27
A
23
Q

Draw the RTS stack at lines:

  1. 6
  2. 12 & 13
  3. 15 & 16
  4. 23&24
  5. 26&27
A
24
Q

What is the general process to follow to setup a subroutine call and make use of the frame pointer?

A

BEFORE the subroutine call (forming the activation record):

  1. Push arguments onto the RTS before the subroutine call. The caller does this
  2. Set aside space on the stack for return values if necessary. The caller does this

INSIDE the subroutine:

  1. Save the value of the frame pointer and then set it to point to the last item put on the activation record.
    1. Take the value of R6 and add 1 to it to get the new frame pointer, which we store in R5
  2. Push any other register’s values onto the stack as necessary
  3. If you want to set aside space for n local variables, you just subtract n from the stack pointer R.
  4. Write subroutine Code

INSIDE the END of the subroutine:

  1. Before the RET instruction, restore the saved register’ values and adjust the stack pointer R^ as necessary. At this point the values of the frame pointer R5 and the stack pointer R^ should have the same value as it had right before the start of the subroutine

Outside the subroutine (back at the caller)

  1. In the caller, adjust the stack point R6 to remove arguments and return value(s) from the stack, as needed.
25
Q

The the RTS throughout this program

A
26
Q

What making a subroutine call inside a subroutine, what needs to be done, and how does that look?

A

Register R7 holds the RET value for PC

Before calling a subroutine from the current subroutine, push R7 onto the RTS before pushing arguments onto the RTS

Upon return from the call, pop the arguments and then restore R7 using the saved value on RTS

;save R7 onto RTS

ADD R6,R6,#-1

STR R7,R6,#0

;push argument onto stack

Add R6,R6,#-1

STR R2,R6,#0

ADD R6,R6,#-1 ; set aside one work on stack for return

JSR Sum

LDR R0,R6,#0 ;get return value of fundtion

ADD R6,R6,#2 ; remove space allocated for the arguments

LDR R7,R6#0 ;restore R7 for ret

ADD R6,R6#1 ; reduce the stack

{restore other registers}

27
Q

Write the simple program that calls a recursive subroutine withing a sub routine

A
28
Q

What is the keys thing to remember about buses?

A

The key point to remember about a bus that is shared by the multiple modules it that only one module at a time can “use” the bus.

Having a lot of devices on a bus can lead to propagation delays

29
Q

What is the difference between Asynchronus and Synchronus timing of a bus

A

Synchronous control:

  • Events are determined by a clock (a bus clock)
  • This clock signal is one of the lines of the control lines
  • All devices can read the clock signal
  • Operations are usually started on the rising edge of the clock
  • Timing is important to ensure that all signrals are stable before being processed
  • Geared towards slowest device on te bus
  • One advantage is that it’s simple
  • Disadvantages
    • Everything must be done in multiple of clock cycles
    • Faster devices run slower than is possible, the bus runs at the slowest speed

Asynchronous control:

  • Does not use a clock unlike in synchronous mode
  • Uses a handshaking protocol to coordinate activities
  • bus master and bus slace speeds to the bus speed for individual bus transactions
  • flexible and expandable
  • One drawback is that it’s more complex and costly, requires a processor to deal with teh complexity.
30
Q

What is the difference between centralized bus arbitration and decentralized arbitration?

A
31
Q

What is the instruction word for:

0x9aAFF

A
32
Q

What is the instruction word for 0xF025

A

Comp 2280 Comp Sys (10 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions