Enzyme Activity & Rate Equations Flashcards
(26 cards)
What happens to the concentration of single substrate to single product reaction as it progresses?
substrate declines and products increase in a linear fashion

define an equation for the general velocity of a single reactant to single product reaction
-∆[S]/∆t because substrate is decreasing, equals ∆[P]/∆t because product is increasing at the same rate

What is the effect of additonal concentration of enzymes on product formation?
Linear increase, each enzyme of the same type reacts at the same pace

As concentration of [S] increases with constant concentration of [E], how does the reaction proceed?
V changes in a hyperbolic (non-linear) fashion.
At low [S], velocity is linear as all enzymes are not yet bound
At high [S], activity levels off due to enzyme saturation. No additional [S] can be converted until existing enzymes turn over S into P

Vmax
Vmax = k2[E]t
All enzymes are bound and turning over substrate to product (fully saturated)
Maximal rate of product formation
Direct effect on turnover number (kcat = Vmax/[E]t), the number of S molecules converted to P molecules per enzyme per unit time
Because all enzymes are bound to substrate during Vmax, [E]t = [ES], so the first-order rate-limiting step k2[ES] is equivilent to k2[E]t which is equivilent to Vmax

What is the mathematical expression for velocity of unimolecular reaction: A ⟶ B?
Rate of the decrease of [A] over time. Directly proportional to amount of reactant, rate constant ( k ) is first-order
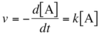
What is the mathematical expression for velocity of bimolecular reaction: A + B ⟶ C?
Rate of the decrease of [A] or [B] over time (equivalent because of the stoichiometry of the reaction, 1 A with 1 B). Directly proportional to amount of reactant, rate constant ( k ) is second-order because velocity depends on two reactants
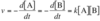
What are the assumptions made in Michaelis-Menten kinetics?
Stoichiometry of S and P are 1:1
k2 is irreversable and the rate limiting step
Steady-state conditions in which the enzyme is saturated with substrate, so that once ES ⟶ E + P, the free enzyme is immediately re-bound to substrate reforming the ES complex, so that there is essentially no free enzyme in solution.
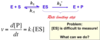
What is the mathematical expression for velocity of a Michaelis-Menten reaction: E +S ⇌ ES ⟶ E + P?
Velocity is the rate at which we increase the concentration of product over time
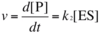
What is the limitation in measurement that Michaelis-Menten kinetics attempts to overcome?
We can measure total amount of substrate [E]t, but [ES] concentration is difficult to measure in the lab, so determining d[P]/dt = k2[ES] for the reaction E + S ⇌ ES ⟶ E + P is not possible. Because we assume that k2 is irreversible, we can measure [ES] indirectly from the formation of ES ( rate1 = k1 [E][S] ) less the depletion of ES ( rate-1 = k-1 [ES] and rate2 = k2 [ES] ).

Explain how Michaelis-Menten kinetics determines the velocity of the reaction
E + S ⇌ ES ⟶ E + P
Velocity of the reaction equals change in product over change in time. We have already determined that our reaction is a first-order reaction dependent on k2 and concentration of ES. But if we cannot measure ES, how can we determine rate of reaction?
v = d[P]/dt = k2[ES] ?
Because we assume that k2 is irreversible, we can measure [ES] indirectly from the formation of ES ( rate1 = k1 [E][S] ) less the depletion of ES ( rate-1 = k-1 [ES] and rate2 = k2 [ES] ).
Steady-state conditions are those in which the enzyme is saturated with substrate, so that once ES ⟶ E + P, the free enzyme is immediately re-bound to substrate reforming the ES complex. There is essentially no free enzyme in solution, so
d[ES]/dt = 0
meaning that ES concentration does not change. Because the concentration of ES does not change over time due to the steady-state assumption, k1 [E][S] - k-1[ES] - k2[ES] = 0.
The concentration of unbound enzyme must be the remainder of the total amound of enzyme less that bound in ES complex, so [E]t-[ES] = [E].
- k*1 ([E]t-[ES])[S] - k-1[ES] - k2[ES] = 0.
- k1 ([E]t-[ES])[S] = [ES] (k*-1 + k2)
(k-1 + k2)/k1 = KM
[E]t[S] - [ES][S] = [ES]KM
[E]t[S] = [ES][S] + [ES]KM
[E]t[S] = [ES] ([S] + KM)
([E]t[S])/([S] + KM) = [ES]
We now have a formula for the concentration of ES, which allows us to determine the velocity of our first-order reaction with respect to our rate-limiting step, k2[ES]
Because all enzymes are bound to substrate during Vmax, [E]t = [ES], so the first-order rate-limiting step k2[ES] is equivilent to k2[E]t which, being our rate-limiting step, is equivilent to Vmax

Explain how [E], [ES], [S], and [P] change graphically over time in a steady-state reaction.

When plotting initial velocity vs. substrate concentration what kind of plot must you get?
A hyperbola

Explain the meaning of KM in relation to substrate affinity
KM is a ratio between the rate ES disappears and the rate ES forms.
If an enzyme has a high affinity for its substrate, k1 will increase, lowering KM.
Low KM = high affinity
High KM = low affinity
The faster the velocity of the reaction, the sooner 1/2 Vmax is reached, and the smaller the value of KM
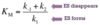
Turnover number
kcat = Vmax/[E]t
Turnover number is the number of S molecules converted to P molecules per enzyme per unit time (measured in s-1). A normalised number that allows for comparison between different enzymes at any concentration.
Explain the meaning of KM beyond the dissociation constant
KM = (k-1 + k2)/k1 = k-1/k1 + k2/k1 = Kd + k2/k1
Because of the additional term k2/k1, KM is not simply a measure of dissociation constant (substrate affinity).
Describe the relationship between KM and Vmax
When substrate concentration is equal to the Michaleis-Menten ES dissociation equilibrium ( [S] = KM ), velocity of the reaction is half-maximal ( 1/2 Vmax )

What is the Michaelis-Menten dervied expression for velocity (Vo) of a enzyme reaction E + S ⇌ ES ⟶ E + P?

Explain KM in relation to substrate affinity
If an enzyme has low KM, it will have high substrate affinity and bind its target even at low substrate concentrations.
On a high level, KM is a measure of the amount of substrate required for significant catalysis to occur. If substrate concentration drops below KM, not much product over time.
Often, KM provides an approximation of substrate concentration in vivo ( [S] ≤ KM )

kcat
kcat = Vmax/[E]t
Turnover number is the number of S molecules converted to P molecules per enzyme per unit time (measured in s-1). A normalised number that allows for comparison between different enzymes at any concentration.
kcat/KM
A measure of catalytic efficiency, as kcat (k2 or rate-limiting step at very high [S]) increases or KM (ES complex binding disociation constant) decreases, efficiency increases kcat/KM becomes greater
Lineweaver-Burk equation as it relates to graphing
1/Vo vs. 1/[S]
Double reciprocal of Michaelis-Menten equation
y-intercept is inverse of Vmax (1/Vmax)
x-intercept is negative inverse of KM (-1/KM)
slope is KM/Vmax

Lineweaver-Burk y-intercept is…
inverse of maximum velocity (1/Vmax)

Lineweaver-Burk x-intercept is…
negative inverse of ES complex dissociation constant (-1/KM)





