Critical Numbers Flashcards
What are the target and sample populations?
- Target population = larger population
- Sample population = sub-set of target population as we can’t sample everyone
What are the 4 main types of bias?
- Sampling bias = individuals more/less likely to be included
- Recall bias = cannot remember specifics
- Social-desirability bias = study group tell us incorrect information due to societal pressure
- Information bias = measurement error
What are the 3 types of study designs?
- experimental (researcher changed something) vs. observational (researcher has not intervened, just observed)
- retrospective (look back into past, subject to bias) vs. prospective (collect information at start and follow up over time)
- individual vs. population
What is a case-control study? What are its strengths and weaknesses?
- Find people with a disease, look back in time and see whether they were exposed to risk factor in question.
- Retrospective
Positives
- Works well for investigating rare outcomes
- Relatively fast/cheap (no follow up)
- Few ethical considerations
Negatives
- Cannot prove causation/eliminate confounders
- Can be difficult to establish order of events
- Possibilities for bias (recall bias)
- Can only investigate a single disease
What is a cross-sectional study? What are its strengths and weaknesses?
•Take a sample, see who has the disease right then and there
Positives
- Relatively fast/cheap (no follow up)
- Few ethical considerations
- Generates hypotheses
Negatives
- Cannot prove causation/eliminate confounders
- Less suitable for rare disease
- Difficult to get an understanding of order of events
- Sample bias (when you do the study)
What is a cohort study? What are its weaknesses?
- Collect information from a sample, some with exposure, some do not (none should have the outcome).
- Follow-up over time and see if there is a link between exposure and outcome
- Prospective
Positives
- Few ethical considerations
- Clarity on event sequence
Negatives
- Cannot prove causation/eliminate confounders
- Not suitable for rare disease or when disease takes a long time to develop
- Time consuming/expensive
- Difficulty following up
- Patients can change behaviours in the cohort
What is randomised controlled trial (RCT)? What are its strengths and weaknesses?
- Multiple groups (referred to as arms), give each different exposures and compare outcomes.
- We can balance arms by matching, randomising, cross-over, placebos, blinding
Positives
- Considered gold standard, can prove causation by eliminating confounders…
- Particularly with extensions (cross-over trial)
- Random (less bias)
Negatives
- Not suitable for rare outcome or when outcome takes a long time to develop
- Time consuming/expensive
- Often unethical
- Issues with people following up, compliance etc.
What is a crossover trial? What are its weaknesses?
- Extension of RCT. Everyone has all arms of trial
- Weaknesses = more technical analyses, not always suitable (even if standard RCT is)
What is an ecological study? What are its strengths and weaknesses?
- Massive sample (if not whole population) by looking at data previously collected to look at prevalence, trends and correlation
- Look at populations, not individuals
Positives
- Fast/cheap
- Very large sample (small standard error)
- Easy to do
- Good first step to generate hypothesis
Negatives
- You do not know how data was collected (variation/bias)
- Often absent/inconsistent/incorrect data – variation in diagnosing criteria
- Cannot prove causation
Ecological fallacy – where there is a correlation between predictor and outcome, but this does not mean causation.
Explain what the ecological fallacy is.
The ecological fallacy occurs when you make conclusions about individuals based only on analyses of group data. Just because two things are linked, it doesn’t imply a causal relationship
What is a sample? What is the difference between the target population and the sample population?
•A sample is a group we are using to represent the population.
–Target population – the population the sample represents
–Sample population – the people whom data is collected
The sample population should generalise the target population.
What are the five main types of sampling?
- Random sampling - random number generator, “draw a name out of a hat”. Usually preferred way of sampling
- Systematic sampling - count of the list and every “k”th element is taken
- Convenience sampling - The first people who approach you are used. Easiest technique but likely the worst
- Cluster sampling:
●Divide the population into groups, usually geographically
●Each group is called a cluster, or block
●Clusters are randomly selected, each element in the selected cluster used
- Stratified sampling:
●Divide the population into groups/strata, based not on geography, but some characteristic, e.g. males and females
●A sample is taken from each of these strata using either random, systematic or convenience sampling
What are the 6 main types of bias?
- Sampling bias – sample is not representative of the target population (encompasses other forms of bias)
- Recall bias – people fail to remember specifics innocently
- Social-desirability bias – incorrect information is given due to societal pressure
- Information bias – where data is consistently measured wrong (may be referred to as observation bias)
- Volunteer bias – volunteers for a study often aren’t representative
- Produced bias – subjects in different arms are treated differently
What are 3 other forms of bias that are related to screening?
•Selection bias - people who sign up for screening programmes are not representative of the whole population (higher/lower risk)
–E.g. women in higher socioeconomic groups more likely to attend cervical cancer screening, who are at lower risk
•Lead time bias - screening improves survival length?
–Maybe no, just detected illness sooner
•Length-time bias - screening improves survival length?
–Maybe no, people who survive longer are more likely to be picked up by screening
What is a confounding factor?
- A confounding factor has to be related to the outcome, and the characteristic of interest (exposure)
- Examples:
- There is a high rate of lung cancer among those who have breath mints. Confounder is smoking.
- There are high rates of cancer among people in care homes. Confounder is old age.
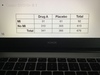
Which type of study design below would be best to investigate the following;
“Identify patients who have had previous MIs and compare their diet, smoking habits and exercise activity with people that are similar but have not suffered previous MI?”
A. Ecological study
B. Cohort study
C. Cross sectional study
D. Longitudinal study
E. Case control study
Answer: E, take the group of individuals who have had heart attacks and look back in time to investigate diet smoking habits and exercise, then do the same for the group who have not suffered heart attacks
A research group wants to estimate the UK national prevalence of coeliac disease. What study design would be most appropriate?
A. Cohort
B. Randomised control trial
C. Cross sectional
D. Longitudinal
E. Case control
Answer: C – Cross sectional, gives a snapshot of prevalence with no reference to time
To calculate the average 100m sprint time, a research group advertises they are looking for participants to run around a track and select participants by a convenience sample.
Which type of bias is this sampling method subject to?
A. Volunteer bias
B. Recall bias
C. Lead time bias
D. Misclassification bias
Answer: A – people who enjoy exercise are more likely to volunteer for the study than those who are not, thus the sample is not entirely representative
To draw a sample from primary school children, researchers line children up and count off the children 1, 2, 3, 1, 2, 3… placing them into 3 different groups
Which term best describes this form of sampling?
A. Random sampling
B. Systematic sampling
C. Convenience sampling
D. Cluster sampling
E. Stratified sampling
B. Count of the list and every “k”th element is taken, here K is 3
A study is designed to examine the relationship between blood pressure (BP) and occupation group. If age is a confounder, then:
- A. Age is linked to diet, and diet affects BP
- B. Different occupations will have different ages, BP will change with age
- C. Younger and older people have the same occupations
- D. Different occupations have similar age groups
B
Which of the following is true of observational studies?
- A. They can have retrospective studies
- B. They are always shorter than an experimental study
- C. They are more powerful than experimental studies
- D. Participants must be randomised into groups before analysing the data
A
University students with insomnia were randomly assigned with a simple randomisation (flip of a coin) to receive either CBT or usual care. This randomisation method ensures:
- A. Each student has an equal chance of being in any treatment group
- B. The student is unaware of the treatment group to which they are assigned
- C. The same number of students will be allocated to each group
- D. Although individuals receive different treatments, each student will be allocated to the treatment most likely to benefit them
A
Sampling bias occurs when:
- A. Certain individuals are more likely to be included in the study than others
- B. 40% of the original sample drop-out of the study at random
- C. Observational studies are used instead of RCTs
- D. The researcher is not blinded within the study
A
In a cohort study:
- A. It is possible to look at a range of outcomes
- B. We use a snapshot of time
- C. We can examine very rare diseases
- D. We don’t worry about confounding
A
A case-control study:
- A. Can often suffer from a loss to follow-up
- B. Is the type of study where individuals are initially selected on the basis of their exposure status, not their outcome
- C. Has an advantage as it allows researchers to look at a range of outcomes
- D. Can often suffer from recall bias
D
Match the study design with the most appropriate description.
- A. Cohort study
- B. Case-control study
- C. Ecological study
- D. Cross-sectional study
1. Carries out in a snap-shot of time without follow up of subjects or looking back in time
2. Collect information now and follow subjects up over time to explore outcomes
3. Collect information on an outcome now, and look back in time to see when exposures were experienced - Information on groups of individuals (e.g. countries) rather than individual level data
1 = D
2 = A
3 = B
4 = C
What are the five steps of Evidence Based Medicine?
- Asking focused questions (use PICO questions: population, intervention, comparator + outcome)
- Finding the evidence
- Critical appraisal (how valid + reliable? Don’t take everything at face value)
- Making a decision
- Evaluating performance
Before any of this, make sure the answer isn’t already out there.
What is PICO?
A way of generating a research question.
- P – patient of population
- I – intervention or indicator (exposure, treatment or procedure)
- C – comparison or control (a group compared against the intervention)
- O – Outcome (end-point of interest)
An example of a research question formed with PICO:
“Is living alone (I) more likely to cause clinical depression (O) in adults aged 20-40 (P) compared to individuals living with 1 or more people (C)?”
What is a variable? What are the two categories of variables?
Variable = quantitative measure of something that varies. Categoric = individuals fall into one of several categories. Numeric = variable measured on a numerical scale
What are the different types of categoric variables?
- Binary = only 2 categories (yes/no)
- Ordinal = >2 categories, ordering (low/medium/high)
- Nominal = >2 categories, no ordering (hair colour)
What are the different types of numeric variables?
- Discrete = distinct number of values, e.g. age in years
- Continuous = any value within a particular range, e.g. blood pressure
How can we display categorical data?
- Categorical data (nominal, ordinal & binary) is normally summarised in terms of frequency.
- For this reason, bar charts and pie charts are commonly used.
- Discrete numerical data can also be displayed via bar and pie charts if it is appropriate to do so.
What types of variables are the following?
- Weight
- Eye colour
- Shoe size
- Social class
- Age
- Is Warfarin prescribed?
- Weight - Continuous
- Eye colour - Nominal
- Shoe size - Discrete
- Social class - Ordinal
- Age - Continuous
- Is Warfarin prescribed? - Binary
What is descriptive statistics? What are the categorical variables used?
- Collection of statistical measures used to describe the data sample we have
- Probability/risk = outcome number / total (0 to 1)
- Percentage = 0 to 100
- Rate = number of times something happens per a quantified (x per 100 people) (0 to infinity)
- Odds = probability of occurence / probability of non-occurence
A study is done to compare the survival rates of various treatments for prostate cancer within a cohort of 695 patients. 348 patients were managed via Watchful Waiting (WW). Of these, 31 patients died. 347 patients were managed via Radical Prostatectomy (RP). Of these, 16 patients died. What are the odds of death from prostate cancer with WW and RP?
WW odds (using populations) = 31 / (348-31) = 0.097….
RP odds (using risks) = (16/347) / (1 - (16/347)) = 0.048….
We can then use these to find the odds ratio which is calculated in the same way as a risk ratio:
The odds ratio of death from prostate cancer with WW compared with RP = (0.097..)/(0.048..) = 2.02
The odds of death from prostate cancer are 102% higher with WW compared to RP
What is the absolute risk difference?
The difference between two risks
A study is done to compare the survival rates of various treatments for prostate cancer within a cohort of 695 patients. 348 patients were managed via Watchful Waiting (WW). Of these, 31 patients died. 347 patients were managed via Radical Prostatectomy (RP). Of these, 16 patients died. What is the Absolute Risk difference of death from prostate cancer with WW compared to RP?
- Risk of death in WW group is 31/348 = 0.089
- Risk of death in RP group is 16/347 = 0.046
- Therefore the Absolute risk difference is 0.089 - 0.046 = 0.043 = 4.3%
- Translated in The risk of death from prostate cancer was 4.3% greater with WW than RP
A zoo has 4 tigers and 10 bears and tests them all for a particular disease due to a recent outbreak. It is discovered that 1/4 tigers and 1/10 bears are carrying the disease. Calculate the risk ratios and odds ratios for both carrying the disease and not carrying the disease.
- The risk ratio of disease in tigers compared to bears is: 1/4 ÷ 1/10 = 2.5
- The risk ratio of non-disease in tigers compared to bears is: 3/4 ÷ 9/10 = 0.833
- The odds ratio of disease in tigers compared to bears is: 1/3 ÷ 1/9 = 3
- The odds ratio of non-disease in tigers compared to bears is: 3/1 ÷ 9/1 = 0.3333 = ⅓
What does 1/ARD give us?
- NNT/H = 1/ARD
- Number Needed to Treat (NNT) or Harm (NNH) is the number of patients who must (on average) be treated with a specific therapy for one of them to benefit or be detrimentally affected respectively over the other treatment.
- In the previous example, the ARD was 0.043. The NNT/H is 1/0.043 = 23.25581…. = 24 patients. THE NNT/H MUST ALWAYS BE ROUNDED UP!
- 24 patients need to be treated with RP over WW to prevent 1 additional death prostate cancer OR 24 patients need to be treated with WW over RP to cause 1 additional death from prostate cancer
Example. Calculate probability, percentage, risk and odds for both Drug A and Placebo.
Drug A:
- Probablility = 31/341 had MI = 0.091
- Percentage = 9.1%
- Rate = 9.1 MI’s per 100 people / 91 MI’s per 1000
- Odds = 31/310 = 0.1
Placebo:
- Probability = 61/366 had MI = 0.167
- Percentage = 16.7%
- Rate = 16.7 MI’s per 100 people / 167 MI’s per 1000
- Odds = 61/305 = 0.2
It’s not sufficient to say that ‘one looks more effective’ when comparing statistics. What 3 methods do we use to compare statistics?
- Risk difference, e.g. Placebo - Drug A = 0.076 or 7.6%, so risk with Placebo is 7.6% higher than with Drug A
- Risk Ratio = Group A/Group B, numerator = focus. 3 potential outcomes: >1, 1, <1. Always compared to 1, e.g. Placebo/Drug A = 0.167/0.091 = 1.835, so risk of MI in Placebo is increased by 0.835 compared to Drug A. Can make Drug A the focus: Drug A/Placebo = 0.091/0.167 = 0.545, so risk of MI in Drug A group decreased by 0.455 compared to Placebo
- Odds ratio = odds in Group A / odds in Group B. 3 potential outcomes: >1, 1, >1. Always compared to 1, e.g. Placebo/Drug A = 0.2/0.1 = 2, so odds of MI in Placebo increased by 1, or 100% compared to Drug A. Making Drug A the focus: Drug A/Placebo = 0.1/0.2 = 0.5, so odds of MI in Drug A decreased by 0.5, or 50% compared to Drug A
- RR<
- Misleading: RR can be 2, but risk difference can be 0.00015, e.g. 30/100000 compared to 15/100000
How can we display numerical data?
Numerical data (mainly continuous) must be displayed using alternative graphs to account for the variable nature of the data.
The main types of graph which are used are:
- Histograms - histograms are essentially continuous boxplots where a bar covers a range as opposed to 1 singular value
- Box and Whisker plots - great for comparing a continuous variable between multiple different groups. Also great for summarising continuous data as it is non-normally distributed on a histogram
- Scatter plots - usually used when displaying 2 continuous variables against each other. Frequently used when assessing correlation and regression
Why is the median sometimes better than the mean? What is skewness?
If we have outliers, the median gives a better representation. Right skew = outlier lies to right of curve, left skew = outlier lies to left of curve
When is the inter-quartile range especially useful?
Especially useful when the data is not normally distributed, i.e. skewed
What are the three main measures of spread?
- Range = largest - smallest
- Inter-Quartile Range = 75th centile - 25th centile, associated with median, most representative, middle 50%
- Standard Deviation = measure of how spread out the values are (average distance from the mean). Affected by extreme values, but also is more powerful as uses all of the values. Cannot use it when we have a skewed distribution.
- Symmetric distribution = mean + standard deviation
- Non-symmetric dsitribution (skewed) = median + IQR
What is the standard error? How is calculated?
- The standard error is the standard deviation of all the sample means
- The standard error (se) is an estimate of the precision of the population parameter estimate that doesn’t require lots of repeated samples. It provides a measure of how far from the true value the sample estimate (usually the mean) is likely to be.
- The standard error assumes that the data is normally distributed and there is a sufficient sample size
- Standard error: S / square root of n
What is the normal distribution?
- Certain numeric variables, when plotted, follow a normal distribution (symmetric). Most people have values in around the mean, and a few extreme, but roughly the same either side. 1 SD either side of mean = 68%, 1.96 SD either side of mean = 95% of sample
- Explained by two parameters: mean + standard deviation
How can we work out where the bottom 2.5% lies? How about the top 2.5%?
If mean = £24,991 + SD = £1,574:
mean - 1.96xSD = 24,991 - (1.96 x 1,574)
= 24,991 - (3,085) = £21,906
Top = mean + 1.96xSD = 24,991 + (1.96 x 1,574)
= 24,991 + (3,085) = £28,076
So between £21,906 and £28,076 is roughly 95% of observed values
We’ve looked at comparing two categoric variables. How about comparing one numeric and one categoric variable or two numeric variables?
- Differences in means/medians (mean if both are normally distributed, median if any of the groups not normally distributed, e.g. normally distribution and a right skew
- Comparing two numeric variables = Pearson’s correlation coefficient (r between -1 and +1). +1 = perfect positive linear association, -1 = perfect negative linear association + 0 = no linear relation at all
The mean of a large sample size:
- A. Is the same as the median if distributed symmetrically
- B. Is greater than the standard deviation
- C. Is calculated by multiplying all values together
- D. Is always a reasonable measure of the centre
A
The inter-quartile range of a set of data represents:
- A. The range inside which the middle 95% of values lie within
- B. The range inside which the middle 25% of values lie within
- C. The range inside which the middle 50% of the values lie within
- D. The spread around the mean in a skewed variable
C
The following is a measure of the spread of a distribution:
- A. Inter-quartile range
- B. Median
- C. Mode
- D. Mean
A
The mean and median values of the data (159, 165, 170, 175 176) are:
- A. 176, 169
- B. 176, 170
- C. 169, 170
- D. 176, 176
C
As the standard deviation of measurements increase:
- A. The mean gets larger
- B. We should use the median
- C. The values become more spread out
- D. The mean becomes more informative
C
The 2 values that are 1.96 standard deviations either side of the mean are:
- A. 99% of the observed sample values
- B. Where all the observed values are for that variable
- C. The range of all potential values for that variable
- D. 95% of the observed sample values
D
The Pearson correlation coefficient:
- A. Takes values between -1 and +1
- B. Is always positive
- C. Is -1 if there is no linear association
- D. Can only be used for binary variables
A
What r value would you give for the second graph?
0.9 - correlation tells us strength of a line, but not which line, e.g. two lines on r = 0.9 but different gradients. Correlations are advanced by REGRESSION
If we increase x by 1 (x + 1), what would the new equations and hence difference be?
- y = a + b (x + 1)
- y = a + bx + b
- Therefore, difference between y = a + bx and y = a + bx + b is b
What can we infer from the b-value for this graph?
If a baby increases temperature by 1 degree, their predicted uninterrupted sleep decreases by 6 hours. y = 224.82 - 5.97x
What type of regression is this?
This has a single continuous variable (sleep time), so is linear regression
How is multiple regression presented?
In a table. In this example:
- there is no significant relationship between birthweight and sleep after adjusting for temperature values
- there is a significant relationship between temperature and sleep after adjusting for birthweight
- accounting for differences in birthweight has not changed our interpretation (although our estimate has changed slightly, -5.97 to -5.46)
Regression isn’t restricted to continuous variables. What happens when we have categorical variables?
- We always have a ‘reference’ category. The coefficient estimate is in comparison to that reference category. For example: north, midlands and south, this would likely be linked to temperature. Pick north as reference value. Note that South has p-value of 0.051, so is borderline. Can’t just say that it’s not statistically significant. These is a significant difference between babies based in the South compared to the North (Southern babies sleep significantly longer)
- There is no significant difference between babies born in the Midland and the North (after accounting for other factors in the model)
The temperature estimate has changed. Is it still significant?
Yes. We are including more factors that explain the relationship with sleep, so the strength of temperauture is likely to diminish. However, it is still significantly associated
