Chapter 8: Evaluating limits Flashcards
(36 cards)
1
Q
Limit Rules
Limit of a constant
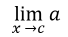
A
The limit of a constant is the constant itself.
= a
2
Q
Limit Rules
Limit of X
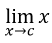
A
The limit of x is the “arrow number”
= c
3
Q
Limit Rules
Constant Multiple Rule

A
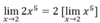
4
Q
Limit Rules
Sum Rule
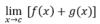
A
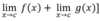
5
Q
Limit Rules
Difference Rule
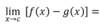
A
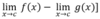
6
Q
Limit Rules
Product Rule
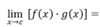
A

7
Q
Limit Rules
Quotient Rule

A

8
Q
Limit Rules
Power Rule
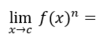
A
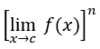
9
Q
Limit Rules
Power Special Rule
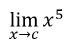
A
c5
10
Q
Limit Rules
Root Special Rule
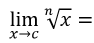
A
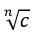
11
Q
Limit Rules
Root Special Rule
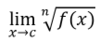
A
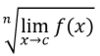
12
Q
Limits to Memorize
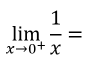
A
∞
13
Q
Limits to Memorize
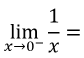
A
-∞
14
Q
Limits to Memorize
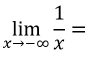
A
0
15
Q
Limits to Memorize

A
0
16
Q
Limits to Memorize

A

17
Q
Limits to Memorize

A
0
18
Q
Limits to Memorize

A
e = 2.718
19
Q
Limits to Memorize

A
0
20
Q
Limits to Memorize

A
1
21
Q
Limits to Memorize

A
cos c
22
Q
Limits to Memorize

A
sec c
23
Q
Limits to Memorize

A
sin c
24
Q
Limits to Memorize

A
csc c
25
**Limits to Memorize**

tan c
26
**Limits to Memorize**

cot c
27
Finding limit with algebra
1. try plugging in arrow number into x
2. If you don't get 0/0, this is the answer
3. If you get 0/0, this is NOT the answer
4. If it's a rational expression
* If it contains square roots, multiply the numerator or denominator by the conjugate
* try to factor
* Cancel any expression from the numerator and denominator
* cancelled expressions = location of holes in the graph
* (x, y) → (arrow number, limit answer)
5. Try substitution of x with arrow number again
6. Check simplified form is a polynomial were x ≠ arrow number
28
Piecewise defined function limits
* check limit
* check 1-sided limits
* left sided limit: x \< n
* right sided limit: x \> n
* check left sided limit = right sided limit
29
Squeeze Thereom
* If functions f and h have the same limit at a
* If function g is between f & h, then g must also have the same limit at a
30
**Limits to Memorize**

∞
31
**Limits to Memorize**

∞
32
**Limits to Memorize**

0
33
**Limits to Memorize**

0
34
**Limits to Memorize**

- ∞
35
**Limits to Memorize**

∞
36
Determining the limit of a function as x approaches infinity or negative infinity is the same as finding the height of the
horizontal asymptote


