Chapter 6: The Trig Tango Flashcards
what is the inverse trig function of
sin30° = 1/2
sin⁻¹1/2 = 30°
- graph of the tangent function
- what is the period of the tangent function

- graph of sin and cos
- period of sin and cos is
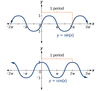
period of periodic function
the length of one of its cycles
sine, cosine, and tangent (and their reciprocals) are periodic functions, which means
their graphs contain a basic shape that repeats over and over indefinitely to the left and right
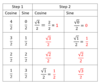
Remembering how to draw unit circle w/16 special angles
Quadrant 1: (x, y), (cosine, sine) coordinates

Step 1:
- Cosine: count down from 4 to 0
- Sine: count up from 1 to 4
- Both: add a denominator of 2 for all
Step 2:
- Make a root of all denominators and simplify
- (1,0) coordinate = 0◦ = 2π
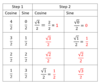
Remembering how to draw unit circle w/16 special angles
Quadrant 2: (x, y), (cosine, sine) coordinates

- Same values of Quadrant 1
- EXCEPT x value is negative
Remembering how to draw unit circle w/16 special angles
Quadrant 4: (x, y), (cosine, sine) coordinates

- Same values of Quadrant 3
- EXCEPT y value is negative
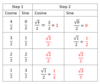
Remembering how to draw unit circle w/16 special angles
Quadrant 3: (x, y), (cosine, sine) coordinates

- Same values of Quadrant 1, BACKWARDS
- x & y value are negative

All Students Take Calculus
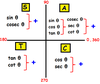
how to draw a right triangle in the unit circle
- put the acute angle at the origin (0,0)
- put the right angle on the x-axis
obtuse angle
Obtuse angles can be from 90 degrees to 180 degrees.
acute angle
- An acute angle (“acute” meaning “small”) is an angle smaller than a right angle.
- The range of an acute angle is between 0 and 90 degrees
where are the cosine, sine and tangent of an angle on a unit circle?
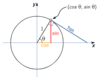
the terminal side of an angle in the unit circle shows the x-coordinate as the angle’s _____ and the y-coordinate as the angle’s _____. To remember this use the mnemonic:
- cosine
- sine
- x & y are in alphabetical order as are cosine and sine

formula to convert degrees to radians and radians to degrees

if 180° = π radians then
- 90 equals _____ of π, or _____ radians
- 60 equals _____ of π, or _____ radians
- 45 equals ______ of π, or _____ radians
- 30 equals ______ of π, or _____ radians
- half, π/2
- third, π/3
- fourth, π/4
- sixth, π/6
360° equals _____ radians, so the unit circle’s circumference is _____. Half a circumference has a length of _____, so 180 equals _____ radians.
- 2π
- 2π
- π
- π
If a circle has a radius of 1, it’s circumference equals ______. if an angle is 30°, it’s _____ of the circle circumference.
- 2π
- 30/360 = 1/12
formula for circumference
C = 2πr
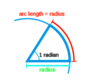
radian
- radian measure of an angle is the length of the arc along the circumference of the unit circle cut off by the angle
- preferred over degrees
To measure an angle in the unit circle, start at the positive _____ axis and go _____ to the ______ side of the angle. If you go _____ instead, you get an angle with a negative measure.
- x
- counterclockwise
- terminal
- clockwise
Unit circle
- used to find values for any size angle
- has a radius of one unit
- set in an x-7 coordinate
- has center at the origin

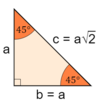
30°, 60°, 90° triangle