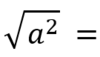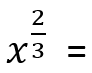Chapter 1 - 4: Calculus PreReqs Flashcards
Calculus PreReqs
solving quadratic equations: completing the square
3x² = 24x + 27
- put the variables on one side and the constant in the other: 3x² - 24x = 27
- divides both sides by coefficient of x²: x² - 8x = 9
- divide coefficient of x by 2 and square it, then add to both sides: x² - 8x + 16 = 9 + 16
- factor left side (factor always has same # from prior step): (x-4)(x-4) = 25 → (x-4)² = 25
- use square root property: x-4 = √25 → x-4 = ±5
- solve: x-4 = ±5 → x = 9 or -1
- The quantity b2 - 4ac, which appears under the radical sign in the quadratic formula
- determines the number and type of solutions
- b2 - 4ac > 0: Two unequal real solutions
- b2 - 4ac = 0: One solution (a repeated solution) that is a real number
- b2 - 4ac < 0: No real solutions
solving quadratic equations: quadratic formula
2x² - 6x + 1 = 12
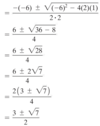
solving quadratic equations: factoring
2x² - 5x = 12
- bring all terms to one side: 2x² - 5x - 12 = 0
- factor: (2x + 3)(x -4) = 0
- set each factor to 0 and solve: 2x + 3 = 0 → 2x = -3 → x = -3/2
- set each factor to 0 and solve: x - 4 = 0 → x = 4
- two solutions: -3/2, 4
differences of two cubes
64x³ - 125
- express each term as the cube of a monomial: 64x³ + 125 = 4x³ - 5³
- convert 4x³ - 5³ to (a³ - b³) = (a - b)(a² + ab + b²)
- (4x - 5)(4x² - 4x5 + 5²) → (4x - 5)(4x² - 20x + 25)
factoring sum of cubes
x³ + 8
- express each term as the cube of a monomial: x³ + 8 = x³ + 2³
- convert x³ + 2³ to (a³ + b³) = (a + b)(a² - ab + b²)
- (x + 2)(x² - x2 + 2²) → (x + 2)(x² - 2x + 4)
quadratic equation
- any second degree (highest power of x is 2) polynomial equation
- 2x² + 5x = 12
x² + bx + c
- when c is positive, find 2 numbers with …
- when c is negative, find 2 numbers with …
- the same sign as the middle term: x² - 5x + 6 = (x - 3)(x - 2)
- opposite signs whose sum is the coefficient of the middle term: x + 3x - 18 = (x + 6)(x - 3)
factoring trinomials steps
x² + 6x + 8
- find the first terms whose product is x²: (x, inside) (x, outside)
- find 2 last terms whose product is 8: 8, 1 or 4, 2 or -8, -1 or -4, -2
- select the terms whose outside product and inside product is 6x: 4, 2
- answer: (x, 4) (x, 2) (outside 2 ⋅ x + inside 4 ⋅ x = 6x)
- x² + 6x + 8
factoring by grouping
x³ + 4x² + 3x + 12
- group terms w/common factor: (x³ + 4x²) + (3x + 12)
- take out GCF: x²(x + 4) + 3(x + 4)
- take out GCF: (x + 4)(x² + 3)
factoring the greatest common factor
x²(x + 3) + 5(x + 3)
- if you are adding, the answer is multiplication
- GCF is (x + 3), so pull it out
- (x + 3)(x² + 5)
factoring the greatest common factor
18x³ + 27x²
- 9 and x² are the greatest integer and expression that divides in 18 & 27 and x² & x³
- 9x²(2x) + 9x²(3)
- 9x²(2x + 3)
what is the degree of the following polynomial:
4x⁵ - 6x³ + x² - 5x + 2
5
degree of a polynomial
the polynomial’s highest power of x
polynomial
- all terms have a variable raised to a positive integral power (no fraction or negative powers)
- just terms with a coefficient
- no logs, sines or cosines allowed
- ex: 4x⁵ - 6x³ + x² - 5x + 2
difference of cubes
(a³ - b³) = (a - b)(a² + ab + b²)
sum of cubes
(a³ + b³) = (a + b)(a² - ab + b²)
a difference of squares (a² - b²) _____ be factored, but a sum of squares (a² + b²) _____
- can
- can’t
factor the following
(3x²)² - (5)²
(3x² - 5)(3x² + 5)
rewrite the following to show a difference of squares (a² - b²)
9x⁴ - 25
(3x²)² - (5)²
LogcC =
1
Logc1 =
0
rewrite log₃81 = x
3ˣ = 81
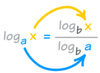
logarithms
2³=8 as log is …
- log₂8 = 3
- log base 2 of 8 = 3
logarithms
rewrite log₂8 with base b
- log₂8 = logb8 / logb8
logarithms
convert log134 to natural logs (base e)
- log134 = loge4 / loge13
- loge4 / loge13 = ln4 / ln13
if you have an even number root/index, you need the _____ value on the answer, because whether the root is positive or negative, the answer is _____. if it’s an odd number root, you don’t need the _____.
- absolute
- positive
- bars
rewrite
(x2)3=
x6
x-4
x2 • x3 =
x5
rewrite as a root
rewrite
x-3 =
1/x3
x0 =
- 1
- if x = 0, then 0⁰ = undefined
is cancelling allowed?
a²b³(xy - pq)⁴(c + d) / ab⁴z(xy - pq)³ + 1
- no
- 1 breaks the chain of multiplication
is cancelling allowed?
a²b³(xy - pq)⁴(c + d) / ab⁴z(xy - pq)³
- yes
- a(xy - pq)(c + d) / bz
multiplication rule for cancelling
can cancel in a fraction only when it has an unbroken chain of multiplication through the entire numerator and denominator
algebraic expression
- anything w/out an equal sign
- if it has an equal sign its an equation
- behave like variables
dividing fractions
- flip the second fraction
- multiply the numerators
- multiply the denominators
multiplying fractions
- multiply the numerators
- multiply the denominators
limits
- the microscope that zooms in on a curve
- zooms in on a curve until its straight
- curves represent changing quantities
convergent series
- you keep adding numbers
- sum keeps growing
- even though you add # forever and sum grows forever, sum of all infinitely is a finite number
divergent series
- series adds up to infinity
- there are some exceptions
slope =
when you zoom in on curves they become _____
straight
integration
adding up small parts of something to get the total
differentiation
finding a derivative
derivative
- slope of a curve or steepness
- simple rate (i.e. miles per hour)
exponential
For any base where b > 0
(bx)y =
bxy
exponential
For any base where b > 0
1 / by =
b-y
exponential
For any base where b > 0
bx / by =
bx / by = bx-y
exponential
For any base where b > 0
bxby =
bxby = bx+y
logarithmic
For any base where b > 0, b ≠ 1
logb 1 =
logb 1 = 0
logarithmic
For any base where b > 0, b ≠ 1
logb x =
logb x = loge x = ln x
logarithmic
For any base where b > 0, b ≠ 1
logb b =
logb b = 1
logarithmic
For any base where b > 0, b ≠ 1
logb xz =
logb xz = z logb x
logarithmic
For any base where b > 0, b ≠ 1
logb 1/y =
logb 1/y = - logby
logarithmic
For any base where b > 0, b ≠ 1
logb x/y =
logb x/y = logbx - logby
logarithmic
For any base where b > 0, b ≠ 1
logbxy =
logbxy = logbx + logby
logarithmic
For any base where b > 0, b ≠ 1
logbbx =
logbbx = x
logarithmic
For any base where b > 0, b ≠ 1
blogbx =
blogbx = x
Natural exponential functions
- b is a positive number not equal to 1
- Inverse of exponential functions
- In the example, function passes through (0,1) and (1,e)
- slope of ex equals the value of ex
- when x = 0, e0 = 1 → value of ex = 1, and slope = 1
- when x = 1, e1 = e → the value of ex = e, and slope = e
- The area up to any x-value is also equal to ex
- only exponential function with the property that the slope of the tangent line at x = 0 is 1, so ex has both value and slope equal to 1 at x = 0
- Simplifies calculations
- Inverse of natural logarithm function: ln(x)
- ln(ex) = x
- They are the same curve with x-axis and y-axis flipped.
- e(ln x) = x
Natural logarithm functions
- with base b = e
- loge(x) which is more commonly written ln(x)
- Inverse of natural exponential function: ex
- e(ln x) = x
- They are the same curve with x-axis and y-axis flipped.
- In the example, function passes through (0,1) and (e,1)
formula for area of triangle
(base • height) / 2
formula for area of square
width • height
Natural logarithm
ln xy =
ln x + ln y
Natural logarithm
ln (x/y) =
ln x - ln y
Natural logarithm
ln |x| =
1 / x
The number e
ln ep =
The number e
ex + y =
exey
The number e
ex - y =
ex / ey
The number e
(ex)p =
exy
The number e
ln (ex) =
x
The number e
b x =
The number e
bx =
simplifying √ of exponents
when the exponent is even
√x6
- divide exponent by 2
- write result outside of √
- leave no variable inside √
√x6
- exponent = 6
- 6 / 2 = 3
- x3√ = x3
- x3 = x6
simplifying √ of exponents
when the exponent is odd
√x3
- subtract one from the exponent
- divide exponent by 2
- write result outside of √
- leave variable inside √ w/no exponent
√x3
- exponent = 3
- 3 - 1 = 2
- 2 / 2 = 1
- 1x√
- 1x√x = x√x
simplifying √ of exponents
√80x3y2
80x3y2
- exponent = 3
- 3 - 1 = 2
- 2 / 2 = 1
x√80xy2
- exponent = 2
- 2 / 2 = 1
xy√80x
- 4 * 4 * 5 = 80
4xy√5x
√80x3y2 = 4xy√5x
exponential growth & decay
f(t) = A0ekt
- A0 = original amount/size at time t = 0
- t = time elapsed
- A = amount at time t
- k
- rate constant
- represents growth rate
- > 0 = growth
- < 0 = decay
Equation for doubling time
time required for a quantity (A0ekt) to double
Equation for half life
