Chapter 7: Limits and Continuity

Question 1

limit

f(x) = 3x + 1

lim_x→2 f(x) = 7

Answer 1

• f(x) = 3x + 1 is the function
• lim_x→2 f(x) = 7
  
  • limit of f(x) as x approaches 2 from the left or the right is 7
• the arrow number (_x→2) gives you a location in the x direction
  
  • if -2, then you are approaching x from the left only
  • if +2 then you are approaching from the right only
  • if you have neither -/+ you are approaching from both sides
• limit (7 in this example) is the y value or height of the function
• you are solving for y value as x approaches 2 from both the left and the right side
• x gets closer and closer to the arrow # but technically never gets there
• having an arrow number = x (variable pass to the function) has no effect to the answer of the limit problem
• limits are used for discontinuous functions that have holes
• x

Question 2

find the limit

lim_x→3 p(x)

Answer 2

• limit does not exist because as x approaches 3 from the left and the right, it doesn’t zero in on the same height
• from the left it jumps on the top line and rises to y=6, closed circle
• from the right it jumps on the bottom line and rises to y=2, open circle
• 6 <> 2
• However, both one-sided limits do exist
  
  • lim_x→3^- p(x) = 6
  • llim_{x→3^{<span>+</span>}} p(x) = 2

Question 3

formal definition of a limit

Answer 3

lim_x→c f(x) exists if and only if

• lim_x→c^- f(x) exists
• lim_x→c⁺ f(x) exists
• lim_x→c^- f(x) = lim_x→c⁺ f(x)
• if you satisfy condition 3 you are good
• undefined <> undefined
• nonexistent <> nonexistent

Question 4

• When we say a limit exists, it means that the limit equals a _____ number
• some limits equal ∞ or -∞, so we say that they _____ exist, aka __ __ __

Answer 4

• finite
• don’t
• DNE

Question 5

asymptote

Answer 5

• line that a curve approaches, as it heads towards infinity
• three types:
  
  • horizontal
    
    • describe the behavior of a graph as the input approaches ∞ or −∞
  • vertical
    
    • describe the behavior of a graph as the output approaches ∞ or −∞
  • oblique
• direction can be positive or negative
• distance between the curve and the asymptote tends to zero as they head to infinity (or −infinity)

Question 6

vertical asymptote of a rational function

Answer 6

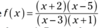
• describe the behavior of a graph as the output approaches ∞ or −∞
• factor the numerator and denominator, if possible
• cancel any factors that are in both the numerator and denominator
• set the denominator equal to zero and solve for x
  
  • x - 3 = 0 → x = 3
  • x + 1 = 0 → x = -1

Question 7

horizontal asymptote of a rational function

Answer 7

• N = degree of the numerator
• D = degree of the denominator
• N < D
  
  • horizontal asymptote is y = 0
  • 2x / 3x² +1
    
    • 1 < 2
    • y = 0
• N = D
  
  • horizontal asymptote is y = ratio of the leading coefficients
  • 2x² / 3x²+1
  • y = ⅔
  • ⅔ is also the answer to the limit
• N > D
  
  • then there is no horizontal asymptote
  • *Slant asymptotes occurs when the degree of the numerator is exactly one more than the degree of the denominator.
  • 2x² / 3x+1

Question 8

slant asymptote

Answer 8

• N = degree of the numerator
• D = degree of the denominator​
• degree of the numerator is exactly one more than the degree of the denominator
• 2x² / 3x+1
• To find equation of the slant asymptote
  
  • divide the fraction and ignore the remainder

Question 9

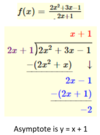
slant asymptote

Answer 9

a graph of a rational function will never cross a vertical asymptote, but the graph may cross a horizontal or slant asymptote. Also, the graph of a rational function may have several vertical asymptotes, but the graph will have at most one horizontal or slant asymptote.

Question 10

formula to approximate the distance that an object falls freely from the rest in t seconds

Answer 10

h(t) = 16t²

​h = distance traveled by object
t = amount of time since the object was dropped

Question 11

distance formula

rate formula

Answer 11

distance = rate * time

rate = distance / time

Question 12

average speed formula

Answer 12

• find the distance traveled for the beginning point
  
  • h(t) = 16t² = 16(1)² = 16
• find the distance traveled for the end point
  
  • h(t) = 16t² = 16(2)²​ = 64
• calculate the average speed

Question 13

average speed formula

what are the x intercepts

Answer 13

• x-intercepts are
  
  • the value of t when h(t) = 0
  • when the object hits teh ground
• to find x-intercepts
  
  • equate function to 0 and solve for t
  • h(t) = -16t² = 96 t
  • 0 = -16t(t - 6)
  • -16t = 0 → t = 0
  • t - 6 = 0 → t = 6
  • object hit the ground at 0 & 6 seconds

Question 14

average speed is the _____ of the ____ ____ joining the points on the graph

Answer 14

• slope
• secant line

Question 15

average / instantaneous velocity formula

Answer 15

Question 16

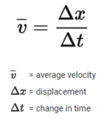
instantaneous speed

how is it determined

Answer 16

• the limit of the average speed as the elapsed time approaches zero
• determined by computing average velocities over intervals [t₀, t₁] that decrease in time
• As t₁ approaches t₀, the average velocities typically approach a unique # → the instantaneous speed
• because the time interval is so short, the avg velocity gives a good approximation to the instantaneous velocity at t = 1

Question 17

instantaneous speed

Answer 17

• the limit of the average speed as the elapsed time approaches zero
• there’s a hole at (1,32) because if you plug 1 into t in the function you get 0/0 which is undefined
  
  • you’re trying to determine an average speed — which equals total distance divided by elapsed time
  • from t = 1 to t = 1 no time has passed, and “during” this point in time, the ball doesn’t travel any distance

Question 18

continuity of polynomial functions

Answer 18

all polynomial functions are continuous everywhere

Question 19

continuity of rational functions

Answer 19

• rational functions: quotient of 2 polynomial functions
• continuous over their entire domain except at x values not in their domain
  
  • (x values where the denominator = 0)

Question 20

the limit at a hole

Answer 20

• the limit at a hole is the height of the hold
• In the graph below
  
  • both functions in have the same limit as x approaches 2; the limit is 4
  • the fact that r(2) =1 and s(2) is undefined are irrelevant
  • for both functions, as x zeroes in on 2 from either side, the height of the function zeroes in on the height of the hole — that’s the limit.

Question 21

slope of the tangent line

Answer 21

• just as the average velocities approach a limit oas t approaches 1, so does the secant line
  
  • both approach the same limit
• slope of secant line approaches slope of tangent line
• instantaneous velocity at t = 1 is the slope of the line tangent

Question 22

derivative-hole connection

Answer 22

• a derivative always involves
  
  • the undefined fraction 0/0
  • the limit of a function with a hole

Question 23

definition of continuity

Answer 23

• a function f(x) is continuous at a point x = a if the following three conditions are satisfied
• if the third condition is met, then the top 2 are met
  
  • left & right sides cannot be DNE or undefined

1. f(a) is defined
2. lim _{x→ a} f(x) exists
3. f(a) = lim _{x→ a} f(x)

Question 24

when does a limit fails to exist

Answer 24

• at a vertical asymptote
  
  • called an infinite discontinuity
  • like at x = 3 on p(x)
• at a jump discontinuity, like where x = 3 on q(x)
• with a limit at infinity of an oscillating function
  
  • like sin x
  • graph goes up/down forever, never zeroing on a single height

Question 25

types of discontinuity

Answer 25

• h, i , j
• (hole) removable discontinuity
  
  • holes in r(x) and s(x)
• infinite discontinuity
  
  • like at x = 3 on p(x)
• jump discontinuity
  
  • like at x = 3 on q(x)

Question 26

3 places the derivative fails to exist

Answer 26

• at any type of discontinuity
• at a sharp point on a function
  
  • cusp or corner
• at a vertical tangent
  
  • cuz slope is undefined

Question 27

evaluating f(x) when it encounters a hole

Answer 27

• can’t return a alue when it encounters a hole
• returns undefined when it hits a hole

Question 28

evaluating a limit when it encounters a hole

Answer 28

returns a value when it encounters a hole

Question 29

how can you tell a rational function has a removeable discontinuity

Answer 29

• removeable discontinuity = hole
• when a function factors and the bottom term cancels
• cancelled term is the hole
  
  • x + 3
  • x + 3 = 0
  • x = -3 ← hole
• After cancelling, you have x - 7

Question 30

how can you tell a rational function has a jump or asymptote

Answer 30

• when a function factors and the bottom doesn’t cancel
• reamining term is a vertical asymptote
• x = 1 cancels → you have a hole at x = -1
• x - 6 didn’t cancel
  
  • x - 6 = 0
  • x = 6 ← asymptote or jump