Chapter 5 - Several Useful Discrete Distributions

Question 1

__ __ __ take on only a finite or countable infinite number of values.

Answer 1

Discrete random variables

Question 2

Three discrete probability distributions serve as models for a large number of practical applications:

Answer 2

Binomial Random Variable

Possion Random Variable

Hypergeometric Random Variable

Question 3

1) The experiment consists of __ __ __.
2) Each trial results in one of two outcomes, __ or __.
3) The probability of success on a single trial is __ and remains __ from trial to trial. The probability of failure is q = 1 – p.
4) The trials are __.
5) We are interested in x, the number of __ in n trials.

Answer 3

1) n identical trials.
2) success (S) or failure (F).
3) p, constant
4) independent
5) successes

Question 4

The Binomial Probability Distribution For a binomial experiment with n trials and probability p of success on a given trial, the probability of k successes in n trials is

Answer 4

Question 5

The Mean and Standard Deviation For a binomial experiment with n trials and probability p of success on a given trial, the measures of center and spread are:

Answer 5

Question 6

You can use the __ __ __ to find probabilities for selected binomial distributions.

Answer 6

cumulative probability tables

Question 7

a model for data that represent the number of occurrences of a specified event in a given unit of time or space

Answer 7

Poisson Random Variable

Question 8

x is the number of events that occur in a period of time or space during which an average of m such events can be expected to occur. The probability of k occurrences of this event is

Mean = ?

Standard Deviation =?

Answer 8

Mean: µ

Standard Deviation: σ = √µ

Question 9

The Hypergeometric Probability Distribution

The probability of exactly k successes in n trials is:

Answer 9

Question 10

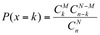
Mean and Variance

The mean and variance of the hypergeometric random variable x resemble the mean and variance of the binomial random variable:

Answer 10

Question 11

Binomial Probabilities can be approximated with Poisson Probabilties when?

Answer 11

np < 7 using µ = np