Chapter 3 - Describing Bivariate Data

Question 1

The resulting data when two variables are measured on a single experimental unit

Answer 1

Bivariate Data

Question 2

You can describe each variable ___, and you can also explore the ___ between the two variables.

Answer 2

individually relationship

Question 3

Bivariate data can be described with? (2)

Answer 3

1) Graphs 2) Numerical Measures

Question 4

When can you use comparative pie charts or bar charts?

Answer 4

When at least one of the variables is qualitative

Question 5

When both of the variables are quantitative? Call one variable __ and the other __. A single measurement is? Can be plotted using?

Answer 5

Call one variable x and the other y. A single measurement is a pair of numbers (x, y) that can be plotted using a two-dimensional graph called a scatterplot.

Question 6

Describing the Scatterplot 1) What __ or __ do you see? 2) How __ is the pattern? 3) Are there any __ __ ?

Answer 6

1) Pattern or Form - straight line up/down - curve/ no pattern 2) Strong -strong, moderate, weak 3) Unusual Observations -clusters or outliers

Question 7

Describe Relationship

Answer 7

1) Positive linear - strong
2) Negative linear -weak
3) Curvilinear
4) No relationship

Question 8

Numerical Measures for Two Quantitative Variables

1) Assume that the two variables x and y exhibit a __ __ or ___.
2) There are two Numberical Measures to describe

Answer 8

1) linear pattern or form
2. a) The strength and direction of the relationship between x and y.
b) The form of the relationship.

Question 9

The strength and direction of the relationship between x and y are measured using this.

equation?

Answer 9

Pearson’s (sample) Correlation Coefficient, r

Question 10

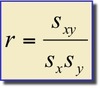
Correlation Coefficient

Sxy =?

Answer 10

Question 11

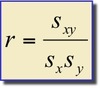
Sx is?

Sy is?

Answer 11

Standard deviation of the x’s = √Sxx

Standard deviation of the y’s = √Syy

Question 12

1) Sign of r indicates?
2) r ≈ 0
3) r ≈ 1 OR r ≈ -1
4) r = 1 OR -1

Answer 12

1) direction of linear relationship
2) weak relationship, random scatter of points
3) strong relationship, either positive or negative
4) all points fall exactly on a straight line

Question 13

The form of the linear relationship between x and y can be described by fitting a line as best we can through the points.

Answer 13

Regression Line

Question 14

Regression Line

Answer 14

y = a + bx

a = y-intercept of the line

b = slope of the line

Question 15

B equation

Answer 15

Question 16

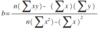
A equation

Answer 16