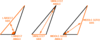Chapter 5 Review

Question 1

perpendicular bisector

Answer 1

a bisector that is also perpendicular

Question 2

Theorem 5.1: Perpendicular Bisector Theorem

Answer 2

If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints of the segment.

EX. If CD is a ⊥ bisector of AB, then AC = BC.

Question 3

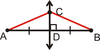
Theorem 5.2: Converse of the Perpendicular Bisector Theorem

Answer 3

If a point is equidistant from the endpoints of a segment, then it is on the perpendicular bisector of the segment.

EX. If AC = BC, then C lies on CD, the ⊥ bisector of AB.

Question 4

concurrent lines

Answer 4

when three or more lines intersect at a common point

Question 5

point of concurrency

Answer 5

the point where concurrent lines intersect

Question 6

circumcenter

Answer 6

the point of concurrency of the perpendicular bisectors

Question 7

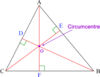
Theorem 5.3: Circumcenter Theorem

Answer 7

The perpendicular bisectors of a triangle intersect at a point called the circumcenter that is equidistant from the vertices of the triangle.

EX. If P is the circumcenter of ΔABC, then PB = PA = PC.

Question 8

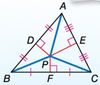
Theorem 5.4: Angle Bisector Theorem

Answer 8

If a point is on the bisector of an angle, then it is equidistant from the sides of the angle.

EX. If CP bisects ∠ACB, PA ⊥ CA, and PB ⊥ CB, then AP = PB.

Question 9

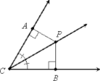
Theorem 5.5: Converse of the Angle Bisector Theorem

Answer 9

If a point in the interior of an angle is equidistant from the sides of the angle, then it is on the bisector of the angle.

EX. If PA ⊥ CA, PB ⊥ CBCP, and AP = PB, then BF bisects ∠ACB.

Question 10

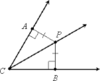
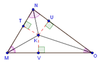
incenter

Answer 10

the point of concurrency for the angle bisectors of a triangle

Question 11

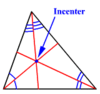
Theorem 5.6: Incener Theorem

Answer 11

The angle bisectors of a triangle intersect at a point called the incenter that is equidistant from the sides of the triangle.

EX. If K is the incenter of ΔMNO, then KT = KU = KV.

Question 12

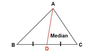
median

Answer 12

a segment with endpoints being a vertext of a triangle and the midpoint of the opposite side

Question 13

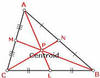
centroid

Answer 13

the point of concurrency on the medians of a triangle

Question 14

Theorem 5.7: Centroid Theorem

Answer 14

The medians of a triangle intersect at a point called the centroid that is two thirds of the distance from each vertex to the midpoint of the opposite side.

EX. If P is the centroid of ΔABC, then AP = ^2/₃AL, BP = ^2/₃ BM, and CP = ^2/₃ CN.

Question 15

altitude

Answer 15

a segment from a vertex to the line containing the opposite side and perpendicular to the line containing that side

Question 16

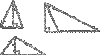
orthocenter

Answer 16

the point of intersection for the lines containing the altitudes of a triangle

Question 17

Inequality

Answer 17

For any real numbers a and b, a > b if and only if there is a positive number c such that a = b + c.

EX. If 5 = 2 + 3, then 5 > 2 and 5 > 3.

Question 18

Comparison Property of Inequality

Answer 18

a < b, a = b, or a > b.

Question 19

Transitive Property of Inequality

Answer 19

1. If a < b and b < c, then a < c.
2. If a > b and b > c, then a > c.

Question 20

Addition Property of Inequality

Answer 20

1. If a > b, then a + c > b + c.
2. If a < b, then a + c < b + c.

Question 21

Subtraction Property of Inequality

Answer 21

1. If a > b, then a - c > b - c.
2. If a < b, then a - c < b - c.

Question 22

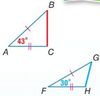
Theorem 5.8: Exterior Angle Inequality

Answer 22

The measure of an exterior angle of a triangle is greater than the measure of either of its corresponding remote interior angles.

EX. m∠1 > m∠2

m∠1 > m∠3

Question 23

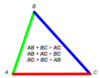
Theorem 5.9: Angle-Side Relationships in Triangles

Answer 23

If one side of a triangle is longer than another side, then the angle opposite the longer side has a greater measure than the angle opposite the shorter side.

EX. CB > AC, so m∠A > m∠B

Question 24

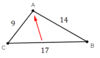
Theorem 5.10: Angle-Side Relationships in Triangles

Answer 24

If one angle of a triangle has a greater measure than another angle, then the side opposite the greater angle is longer than the side opposite the lesser angle.

Question 25

indirect reasoning

Answer 25

Reasoning that assumes that the conclusion is false and then shows tha tthis assumption leads to a contradiction of the hypothesis like a postulate, theorem, or corollary. Then, since the assumption has been proved false, the conclusion must be true.

Question 26

indirect proof; proof by contradiction; proof by negation

Answer 26

In an indirect proof, one assumes that the statement to be proved is false. One then uses logical reasoning to deduce that the statement contradicts a postulate, theorem, or on of the assumptions. Once a contradiction is obtained, one concludes that the statement assumed false must in fact be true.

Question 27

Theorem 5.11: Triangle Inequality Theorem

Answer 27

The sum of the lengths of any two sides of a triangle must be greater than the length of the third side.

Question 28

Theorem 5.13: Hinge Theorem

Answer 28

If two sides of a triangle are congruent to two sides of another triangle, and the included angle of the first is larger than the included angle of the second triangle, then the third side of the first triangle is longer than the third side of the second triangle.

EX. If AB ≅ FG, AC ≅ FH, and m∠A > m∠F, then BC > GH.

Question 29

Theorem 5.14: Converse of the Hinge Theorem

Answer 29

If two sides of a triangle are congruent to two sides of another triangle, and the third side in the first is longer than the third side in the second triangle, then the included angle measure of the first triangle is greater than the included angle measure in the second triangle. Converse of the Hinge Theorem

EX. If JL ≅ PR, KL ≅ QR, and PQ > JK, then m∠R > m∠L.