Chapter 3 Review

Question 1

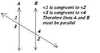
parallel lines

Answer 1

coplanar lines that do not intersect

Example: AB || MN

*Arrows are used to indicate that lines are parallel.

Question 2

skew lines

Answer 2

lines that do not intersect and are not coplanar

EX. Lines n₁ and n₂ are skew.

Question 3

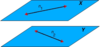
parallel planes

Answer 3

planes that do not intersect

EX. Planes X and Y are parallel

Question 4

transversal

Answer 4

a line that intersects two or more coplanar lines at two different points

Question 5

interior angles

Answer 5

angles that lie between two transversals that intersect the same line

Question 6

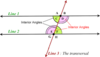
exterior angles

Answer 6

an angle that lies in the region that is not between two transversals that intersect the same line

Question 7

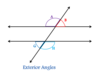
consecutive interior angles

Answer 7

interior angles that lie on the same side of the transversal

Question 8

alternate interior angles

Answer 8

nonadjacent interior angles that lie on the opposite sides of a transversal

Question 9

alternate exterior angles

Answer 9

nonadjacent exterior angles that lie on the opposite sides of a transversal

Question 10

corresponding angles

Answer 10

angles tha tlie on the same side of a transversal and on the same same sides of the intersecting lines

Question 11

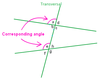
Postulate 3.1: Corresponding Angles Postulate

Answer 11

If two parallel lines are cut by a transversal, then each pair of corresponding angles is congruent.

Question 12

Theorem 3.1: Alternate Interior Angles Theorem

Answer 12

If two parallel lines are cut by a transversal, then each pari of alternate interior angles is congruent.

Question 13

Theorem 3.2: Consecutive Interior Angles Theorem

Answer 13

If two parallel lines are cut by a transversal, then each pair of consecutive interior angles is supplementary.

Question 14

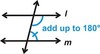
Theorem 3.3: Alternate Exterior Angles Theorem

Answer 14

If two parallel lines are cut by a transversal, then each pair of alternate exterior angles is congruent.

Question 15

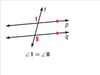
Theorem 3.4: Perpendicular Transversal Theorem

Answer 15

In a plane, if a line is perpendicular to one of two parallel lines, then it is perpendicular to the other.

Question 16

slope

Answer 16

the ratio of change along the y-axis to the change along the x-axis between two points on a line

Question 17

slope formula

Answer 17

Question 18

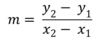
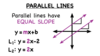
Postulate 3.2: Slopes of Parallel Lines

Answer 18

Two nonvertical lines have the same slope if and only if they are parallel. All vertical lines are parallel.

Question 19

Postulate 3.3: Slopes of Perpendicular Lines

Answer 19

Two nonvertical lines are perpendicular if and only if the product of their slopes is - 1. Vertical and horizontal lines are perpendicular.

Question 20

slope-intercept form

Answer 20

y =mx + b

(m = slope; b = y-intercept)

Question 21

point-slope form

Answer 21

y - y₁ = m (x - x₁)

(m = slope; (x₁,x₂) = any point on the line)

Question 22

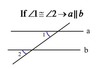
Postulate 3.4: Converse of Corresponding Angles Postulate

Answer 22

If two lines are cut by a transversal so that corresponding angles are congruent, then the lines are parallel.

Question 23

Postulate 3.5: Parallel Postulate

Answer 23

If given a line and a point not on the line, then there exists exactly one line through the point that is parallel to the given line.

Question 24

Theorem 3.5: Alternate Exterior Angles Converse

Answer 24

If two lines in a plane are cut by a transversal so that a pair of alternate exterior angles is congruent, then the two lines are parallel.

Question 25

Theorem 3.6: Consecutive Interior Angles Converse

Answer 25

It two lines in a plane are cut by a transversal so that a pair of consecutive interior angles is supplementary, then the lines are parallel.

Question 26

Theorem 3.7: Alternate Interior Angles Converse

Answer 26

If two lines in a plane are cut by a transversal so that a pair of alternate interior angles is congruent, then the lines are parallel.

Question 27

Theorem 3.8: Perpendicular Transversal Converse

Answer 27

In a plane, if two lines are perpendicular to the same line, then they are parallel.

Question 28

Postulate 3.6: Perpendicular Postulate

Answer 28

If given a line and a point not on the line, then there exists exactly one line through the the point that is perpendicular to the given line.

Question 29

equidistant

Answer 29

the distance between two lines measured along a perpendicular line to the lines is always the same

Question 30

Theorem 3.9: Two Lines Equidistant from a Third

Answer 30

In a plane, if two lines are each equidistant from a third line, then the two lines are parallel to each other.