Chapter 1 Review Flashcards
Undefined terms
Can only be explained using examples and descriptions (ie. point, line, plane)
Point
A location.
Has neither shape nor size.
Named by a capital letter.
Example: point A
• A
Plane
A flat surface made up of points that extends infinitely in all directions. There is exactly one plane through any three points not on the same line.
Named: Plane m, plane ABC
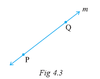
Line
Made up of points and has no thickness or width. There is exactly one line through any two points.
Named: line m, line PQ
Collinear
Points that lie on the same line
Coplanar
points that lie on teh same plane
intersection
the point or set of points shared by two or more geometric figures
P represents the intersection
defined terms
Explained using undefined terms and/or other defined terms
space
a boundless, three-dimensional set of all point; can contain lines and planes
line segment
part of a line that can be measured using two endpoints
between
Point M is between points P and Q if and only if P, Q, and M are collinear and PM + MQ = PQ
congruent segments
segments that have the same measure
distance between points
the length between two points as measured by the absolute value of the difference between their coordinates
Formula d = | b - a |
Distance formula (in a coordinate plane)
irrational number
A number that cannot be expressed as a repeating decimal.
Midpoint
the point halfway between the endpoints of a segment
Midpiont formula (in a coordinate plane)
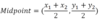
Midpoint formula
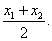
segment bisector
any segment, line, or plane that intersects a segment at its midpoint
ray
a part of a line that has one endpoint and extends indefinitely in one direction
Named by stating the endpoint first and then any other point on the ray
opposite rays
two rays that share the same endpoint, go in opposite directions, and are collinear
EX. BA and BC are opposite rays
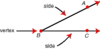
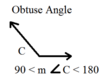
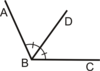
angle
formed by two noncollinear rays that have a common endpoint
sides
the rays that form an angle
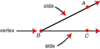
vertex
the common endpoint of an angle
Interior points
points that lie inside of the angle
EX. points A, D, and F
Exterior points
points that lie outside of the angle
EX. points B and C
degree
unit of measure used for angles
EX. 98°
right angle
an angle measuring 90°
acute angle
an angle measuring less than 90°
obtuse angle
an angle measuring more than 90°
angle bisector
a ray that divides an angle into two congruent angles
congruent angles
angles that have the same degree measure
adjacent angles
two angles that lie in the same plane and have a common vertex and a common side, but no common interior points
linear pair
a pair of adjacent angles with noncommon sides that are opposite rays
vertical angles
two nonadjacent angles formed by two intersecting lines; they are congruent
EX. angle 1 and angle 3
complementary angles
two angles with measures that have a sum of 90°
supplementary angles
two angles with measures that have a sum of 180°
perpendicular
lines, segments, or rays that form right angles
polygon
a closed figure formed by a finite number of coplanar segments called sides such that
- the sides that have a common endpoint are noncollinear
- each side intersects exactly two other sides, but only at their endpoints
concave polygon
a polygon for which there is a line containing a side of the polygon that also contains a point in the interior of the polygon
convex polygon
a polygon for which there is no line that contains both a side of the polygon and a point in the interior of the polygon
equilateral
all sides have the same measure
equiangular
all angles have the same measure
regular polygon
polygon is equilateral and equiangular
How many sides does a triangle have?
3
How many sides does a quadrilateral have?
4
How many sides does a pentagon have?
5
How many sides does a hexagon have?
6
How many sides does a heptagon have?
7
How many sides does a octagon have?
8
How many sides does a nonagon have?
9
How many sides does a decagon have?
10
perimeter
the sum of the lengths of the sides of the polygon
circumference
the distance around a circle
area
the number of square units needed to cover a surface
Perimeter of a triangle formula
P = a + b + c
Area of a triangle formula
A = ½bh
Perimeter of a square formula
P = s + s + s + s
Area of a square formula
A = s2
Perimeter of a rectangle
P = 2l + 2w
Area of a rectangle
A = lw
Circumference formula
C = 2πr or C = πd
Area of a circle formula
A = πr2
polyhedron
a solid with all flat surfaces that enclose a single region of space
prism
polyhedron with two parallel congruent faces (called bases) connected by parallelogram faces
pyramid
a polyhedron that has a polygonal base and three or more triangular faces that meet at a common vertex
cylinder
a solid with congruent parallel circular bases connected by a curved surface
cone
a solid with a circular base connected by a curved surface to a single vertex
sphere
A set of points in space that are the same distance from a given point. It has no faces, edges, or vertices.
surface area
a two-dimensional measurement of the surface of a solid figure
volume
the measure of the amount of space enclosed by a solid figure
Surface area of a prism formula
- S = Ph + 2B*
- (P = perimeter of the base; B = area of the base)*
Volume of a prism formula
V = Bh
(B = area of the base)
Surface area of regular pyramid
S = ½Pl +B
(P = perimeter of base; l = slant height; B = area of base)
Volume of reglar pyramid
V = 1/3 Bh
(B = area of base)
Surface area of a cylinder
S = 2πrh + 2πr2
Volume of a cylinder
V = πr2h
Surface area of a cone
S = πrl + πr2
Volume of a cone
V = 1/3 πr2h
Surface area of a sphere
S = 4πr2
Volume of sphere
V = 4/3πr3
