Chapter 4 Review Flashcards
acute triangle
has 3 acute (less than 90°) angles
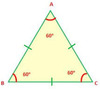
equiangular triangle
has 3 congruent angles
obtuse triangle
has 1 obtuse (more than 90°) angle
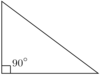
right triangle
has 1 right (exactly 90°) angle
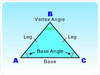
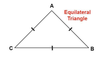
equilateral triangle
has 3 congruent sides
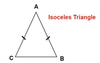
isosceles triangle
has at least 2 congruent sides
scalene triangle
has no congruent sides
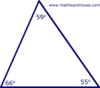
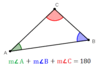
Theorem 4.1: Triangle Angle-Sum Theorem
The sum of the measures of the angles of a triangle is 180.
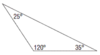
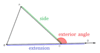
exterior angle of a triangle
formed by one side of the triangle and the extension of an adjacent side
remote interior angles
the angles of a triangle that are not adjacent to a given exterior angle
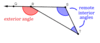
Theorem 4.2: Exterior Angle Theorem
The measure of an exterior angle of a triangle is equal to teh sum of the measures of the two remote interior angles.
EX. m∠4 = m∠1 + m∠2
corollary
a theorem with a proof that follows as a direct result of another theorem
Corollary 4.1: Right Angle Corollary
The acute angles of a right triangle are complementary.
Corollary 4.2: Obtuse Angle Corollary
There can be at most one right or obtuse angle in a triangle.
EX. If m∠B ≥ 90°, then ∠A and ∠C are acute angles.
congruent polygons
all of the parts of one polygon are congruent to the corresponding or matching parts of the other polygon
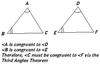
Theorem 4.3: Third Angles Theorem
If two angles of one triangle are congruent to two angles of a second triangle, then the third angles of the triangles are congruent.
Reflexive Property of Triangle Congruence
ΔABC ≅ ΔABC
Symmetric Property of Triangle Congruence
If ΔABC ≅ ΔEFG, then ΔEFG ≅ ΔABC.
Transitive Property of Triangle Congruence
If ΔABC ≅ ΔEFG and Δ EFG ≅ ΔJKL, then ΔABC ≅ ΔJKL.
Postulate 4.1: Side-Side-Side (SSS) Congruence
If three sides of one triangle are congruent to three sides of a second triangle, then the triangles are congruent.
EX. If Side AB ≅ XW,
Side AC ≅ XY, and
Side BC ≅ WY,
then ΔABC ≅ ΔXWY.
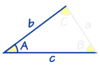
included angle
the angle formed by two adjacent sides of a polygon
EX. ∠A is the included angle of sides b and c
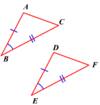
Postulate 4.2: Side-Angle-Side (SAS) Congruence
If two sides and the included angle of one triangle are congruent to two sides and the included angle of a second triangle, then the triangles are congruent.
EX. If Side AB ≅ DE,
Angle ∠B ≅ ∠E, and
Side BC ≅ EF,
then ΔABC ≅ ΔDEF.
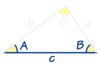
included side
the located between two consecutive angles of a polygon
EX. Side c is the included side
Postulate 4.3: Angle-Side-Angle (ASA)
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
If Angle ∠A ≅ ∠D,
and Side AC ≅ DF,
and Angle ∠C ≅ ∠F,
then ΔABC ≅ ΔDEF.
Theorem 4.5: Angle-Angle-Side (AAS) Congruence
If two angles and the nonincluded side of one triangle are congruent to the corresponding two angles and side of a second triangle, then the two triangles are congruent.
EX. If Angle∠B ≅ ∠E,
Angle ∠C ≅ ∠F ,
and Side AC ≅ DF,
then ΔABC ≅ ΔDEF.
legs, vertex, base, and base angles of an isosceles triangle
legs = the two congruent sides of the triangle
vertex angle = the angle with the sides that are legs
base = the side of the triangle opposite the vertex angle
base angles = the two angles formed by the base and the congruent sides
Theorem 4.10: Isosceles Triangle Theorem
If two sides of a triangle are congruent, then the angles opposite those sides are congruent.
EX. If AB ≅ AC, then ∠C ≅ ∠B.
Theorem 4.11: Converse of Isosceles Triangle Theorem
If two angles of a triangle are congruent, then the sides opposite those angles are congruent.
EX. If ∠B ≅ ∠C, then AC ≅ AB.
Corollary 4.3: Equilateral Triangle Corollary
A triangle is equilateral if and only if it is equiangular.
EX. If ∠A ≅ ∠B ≅ ∠C, then AB ≅ BC ≅ CA.
Corollary 4.4: Equilateral Triangle Corollary
Each angle of an equilateral triangle measure 60°.
EX. If AB ≅ BC ≅ CA, then ∠A = ∠B = ∠C = 60°.
