Chapter 5 Flashcards
Sample Statistics
Summarizes sample characteristics
Parameters
Summarize population characteristics
Sample Mean
Mean of the sample,
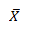
Sample Proportion
Proportion of sample,
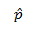
Population Mean
Mean of the population,
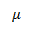
Population Proportion
True proportion, p
Statistic as a RV
Statistic is a random variable and will have a distribution assigning probabilities to different samples
Sampling Distribution
Probability distribution of sample statistics, tells us how much a statistic would vary from sample to sample
Mean of Sample Proportion
Mean p
Standard Deviation of Sample Proportion
SD
When is distribution approximately normal?
When for a sample size n with true proportion p, both np and n(1-p) are greater than or equal to 15
Normal Distribution of Sample Proportion
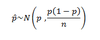
Standard Error
Estimate of standard deviation of sampling distribution
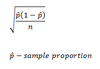
What happens to standard deviation as sample size n increases?
Standard deviation decreases
Smaller the standard deviation…
…closer the sample proportion is to the population proportion
Empirical Rule
Nearly all sample proportions for size n with true proportion p will lie between
Probability with Normal Distribution and pHat
Sample mean distribution centered around…
True population mean mu
Sample mean distribution standard deviation
Sample Mean Normal Distribution
What does increasing sample size n do to sample means?
Vary less and less tending toward true population mean
Central Limit Theorem
As sample size increases, sampling distribution of sample mean tends to a normal distribution, even if population distribution far from bell-shaped
Ensuring normal distribution for standard mean
n greater than or equal to 30
Statistical Inference
Making decisions about parameters using statistics
Point Estimation
Single estimate for population parameter, usually sample mean
Interval Estimation
Form a confidence interval of population parameter within which true parameter value is believed to lie at a certain confidence level
Significance Test
Yields decision on whether claim about value of parameter is supported by data observed from a random sample
C + E Model
Center + Error ; usually C is the sample mean and E is the margin of error
Confidence Level
Level of confidence with which method produces an interval that contains the true parameter value
100% Confidence Level
Not relevant, would be all possible values
Margin of Error
How accurately the statistic estimates unknown parameter
General form of C + E Confidence Interval
Robust
A procedure that performs adequately even when a particular assumption is violated
Standard Error and T-Score as sample size increases (or, if CI decreases)
The two decrease and the margin of error likewise decreases, so the CI gets shorter
How CI changes with fixed sample size if CI increases…
T-Score and margin of error increase so the CI gets wider
How to think about CI
- We are X% confident that the true population mean lies between the lower and upper bounds
- Of 100 X% intervals calculated the same way, we expect X of them to contain the true population mean
- In a long series of repeated trials, X% of the intervals will contain the true population mean
