Chapter 4 Flashcards
(37 cards)
Probability
Mathematics describing random behaviors, measuring chances, and quantifying uncertainties
Random Phenomenon
Situation in which we know what possible outcomes could happen but we don’t know which ones will happen until they occur
Trial
An attempt or random experiment that generates an outcome (flipping a coin once)
Probability as a long-term frequency
The probability of any outcome of a random phenomenon is the proportion of times the outcome would occur in a long series of repeated trials
Long-term frequency example with a fair coin toss
If you were to toss a fair coin, say, a million times, you would tend toward getting heads 1/2 the time and tails 1/2 the time. Thus the probability of getting either can be said to be 1/2.
Sample Space
Set of all possible outcomes
Dice Sample Space
{1,2,3,4,5,6}
Pop quiz example with three questions (C, I) _ _ _
2^3 possibilities since there are 2 choices (Correct, Incorrect) for each of the 3 slots. So there are 8 possibilities in all
Event
Any outcome or set of outcomes of a random phenomenon; subset of sample space
P(A)
Probability of event A
Three Axioms of Probability

Enumeration Method
Find probability of each individual outcome in sample space and add probabilities of each outcomes event A contains
Classical Method
If outcomes are equally likely:

Complement of A
All outcomes in sample space not in A
Complement of A Formula
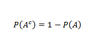
Disjoint Events (Mutually Exclusive)
A and B are disjoint if they share no common outcomes
Disjoint Formula
A and B are disjoint if:

Independent Events
A and B are independent if event A never affects probability of event B and vice versa
Independence Formula
A and B are independent if:

Union of Events
The union of A and B are the outcomes that are in A or B
Union Formula
The union of A and B is found as:

How often are events Independent?
Not often
Independence and Mutual Exclusivity (Disjointness)
They are NOT equal; essentially opposite
Random Variable
A numerical measurement of the outcome of a random phenomenon






