8+9+10 - Dynamic Consequences of Technology Shocks and Possible Pitfalls

Question 1

Which response to a positive technology shock does the RBC model predict?

Answer 1

It predicts positive comovement between productivity, output and employment in response to technology shocks:

aₜ ↑ -> yₜ ↑, nₜ ↑

Question 2

What is the traditional approach to explain business cycle fluctuations in the RBC approach?

Answer 2

second moment matching (model driven by technology shocks vs. data)

Question 3

Which response to a positive technology shock does the NKM (Galí & Rabanal) predict?

Answer 3

It predicts negative comovement between output and employment in response to technology shocks:

aₜ ↑ -> yₜ ↑, nₜ ↓

Question 4

Where does the NKM result of the negative comovement of output and labor in response to technology shocks stem from? (What is the intuition behind it?)

Answer 4

From two equations:

1. yₜ = mₜ - pₜ
2. yₜ = aₜ + n_t

Thus if technology increases, prices drop (but not as much - Calvo pricing). To keep equation 2. valid, then, labor has to decrease.

Question 5

What does the RBC model aim to predict by using the positive comovement between output and labor as response to technology shocks?

Answer 5

generate fluctuations that resemble business cycles

Question 6

Why is it important to examine if the RBC model or the NK model are empirically relevant?

Answer 6

• If the RBC model was empirically relevant, this would imply that there is no scope for economic policy, because business cycle fluctuations would reflect the optimal allocation over time.
• If the NK model is empirically relevant, this implies a need for government intervention, because fluctuations reflect distortions from the optimal allocation. If the frictions in the NK model (rigid prices, imperfect competition) explain large parts of the fluctuations, there is a scope for economic policy (i.e. monetary or fiscal policy) to stabilize fluctuations.

Question 7

Which methods can be used to examine if the models are empirically relevant? How do the results differ?

Answer 7

• Unconditional: Comparison of second moments generated by model with second moments of data.
• Conditional: SVAR analysis.

The finding of the conditional exercise is that the central mechanism of the RBC model (positive co-movement of hours and output) cannot be found in the data.

Question 8

How does the unconditional method used to examine if the models are empirically relevant work? What is problematic about it?

Answer 8

Definition of unconditional method: Compare second moments generated by the model with the second moments of the data (second moments = variance, covariance)

How it is applied: They take residuals that cannot be explained by labour/output and call this the technology shocks, which they feed back into the model.

Problematic: One cannot be sure that the residuals are really technology shocks and not other shocks.

Question 9

How does the conditional method used to examine if the models are empirically relevant work?

Answer 9

Definition of conditional method: SVAR Analysis

How it is applied: They first identify technology shocks and then look at the response of other variables.

Question 10

How can the negative co-movement of output and hours conditional on a technology shock be explained, given that money supply is exogenous?

Answer 10

If money supply is exogenous, money demand is given by:

m_t¯ - p_t = a_t + n_t

(first part of equation is the simple money demand m - p = y,
second part is the production function in euqilibrium y = a + n)

If a_t increases (technology shock), with exogenous m¯ constant and staggered adjustment of p_t (price rigidity), n_t has to decrease for the equation to hold.

Question 11

How can you rewrite the inflation equation below?

Answer 11

Question 12

Where does the inflation equation below originate from?

Answer 12

Question 13

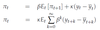
How does the he existence of sticky prices influence what happens after changes in technology, in the NKM?

Answer 13

The existence of sticky prices reduces the fluctuations in output from changes in technology, compared to the fluctuations in flexible price output.

Question 14

What is AR (p)? What are the components?

Answer 14

• univariate autogregressive model

y_t = α₁ y_t-1 + α₂ y_t-2 + … + α_p y_t-p + u_t

where:

• α = coefficient
• p = # lags
• u_t = forecast error

Question 15

What is the reduced form VAR ? What are the components?

Answer 15

• multivariate autogregressive model
• reduced form can only be used for forecast

Y_t = B₁ Y_t-1 + B₂ Y_t-2 + … + B_p Y_t-p + U_t

where:

• Y = vector
• B = matrix
• p = # lags
• Ut = Vector of forecast error

Question 16

Which assumption makes the SVAR structural?

Answer 16

Since all the off-diagonal entries are zero, this assumption implies that the economic shocks ε_t are uncorrelated. Hence we can attach one distinct economic meaning to each.

Question 17

What are the other assumptions that SVAR is based on?

(on top of structural condition)

Answer 17

• Exogeneity: E {u_t x_t-k’} = 0
• Definition: E {u_t u_t’} ≡ Σ
• Relationship between forecast errors u_t & economic shocks e_t: u_t = S e_t

Question 18

How can you indentify the matrix S in the SVAR?

Answer 18

1. u_tu_t’ = Sε_tε_t‘S’
2. Σ = E[u_tu_t’] = E[Sε_tε_t‘S’] = S E[ε_tε_t’] S’
3. Since E[ε_tε_t’] = I: Σ = SS’

In order to compute SS’ from Σ, we need n(n-1)/2 “identifying assumptions” (=restrictions)

Question 19

What are 5 Possible Pitfalls in the Estimation of the Effects of Technology Shocks?

Answer 19

• Are long-run restrictions useful?
• Do capital income tax shocks explain permanent changes in labor productivity?
• Do permanent shocks to labor productivity capture variations in technology?
• How robust is the VAR specification?
• Investment-specific shocks?

Question 20

Explain this possible pitfall in the estimation of the effects of technology shocks:

Do capital income tax shocks explain permanent changes in labor productivity?

Answer 20

1. Assumption of a stationary capital income tax rate may not be justified
2. First impression: non-stationary behavior (graph taken from Galí and Rabanal 2004)
3. Formally: ADF test (unit root test for stationarity) fails to reject the null hypothesis of a unit root (If a time series has a unit root, it shows a systematic pattern that is unpredictable)

Question 21

Explain this possible pitfall in the estimation of the effects of technology shocks:

Do Permanent Shocks to Labor Productivity Capture
Variations in Technology?

Answer 21

1. Assess the plausibility of the technology related interpretation of the VAR shocks.
2. Idea: Examine their correlation with the BFK measure

Question 22

Explain this possible pitfall in the estimation of the effects of technology shocks:

How Robust is the VAR Specification?

Answer 22

First-differencing the (log of) per-capita hours may distort the sign of the estimated response of that variable to a technology shock if that variable is truly stationary.

Question 23

Respond to this possible pitfall in the estimation of the effects of technology shocks:

Are Long-Run Restrictions useful?

Answer 23

Answer: At least they can be rationalized in te context of superlarge DSGE models that are consistent

Question 24

What are the questions that RBC or NK are trying to answer statistically?

Answer 24

• What is the impact of technology shocks on macroeconomic variables?
• What part of the business cycle fluctuations is caused by technology shocks?
• Which model (RBC or NK) is empirically relevant?

Question 25

For the RBC model (e.g. Kydlend + Prescott), what do they do to estimate the impact of technology shocks?

Answer 25

• Compute the Solow Residual = part of output growth that is not explicable by measurable changes in the amount of capital/labor
• use the Solow Residual as exogenous technology process and feed it into the RBC model -> get simulated time series data
• Compute second moments (i.e. variance, covariance) of the simulated data (i.e. output from the model) and compare it with the second moments of the “actual” data (observed in reality)

Question 26

For the RBC model (e.g. Kydlend + Prescott), what do they find?

Answer 26

• The second moments of the simulated data and the actual data are very similar
• They conclude that the RBC model driven by technology shocks is successful in explaining business cycle fluctuations

Question 27

For the RBC model (e.g. Kydlend + Prescott), what are problems with their analysis?

Answer 27

• Further research has shown that the Solow residual is not a good estimate of technology shocks: it contains a lot of other shocks (demand shocks, monetary shocks), not only technology shocks
• In reality, the positive unconditional co-movement of hours+output is driven by a combination of all these shocks