7 - Dynamic Consequences of Shocks

Question 1

Interpret the equation:

Answer 1

Technology
Technology aₜ evolves according to a Random Walk: aₜ = aₜ₋₁ + ϵₜᵐᵘ (where ϵₜᵐᵘ is a technology shock with {ϵₜᵐᵘ} i.i.d. with mean zero). We can transform this process to a stationary process by substracting aₜ₋₁ from both sides:

Question 2

Interpret the equation:

Answer 2

New IS Curve (or Dynamic IS Equation)
As output inherits the non-stationarity of aₜ, we want to work instead with the output gap, which is stationary. We use the New IS Curves (with ṝₜ = ρ, σ = 1):

Question 3

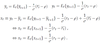
Interpret the equation:

Answer 3

New Keynesian Phillips Curve

Question 4

Interpret the equation:

Answer 4

Production function:

Question 5

Interpret the equation:

Answer 5

Real interest rate definition.

Question 6

Interpret the equation:

Answer 6

We use Galí’s definition of the money demand in logs.

We assume η = 1 and substract natural output from both sides. Then, we multiply the last term on the RHS by 4 in order to annualize the interest rate

Question 7

Interpret the equation:

Answer 7

Accounting identity
If we take the difference over time of MPYₜ, we get:

Question 8

What are the steady state values of the variables in the stationary model?

Answer 8

As all variables are in percentage deviations from the zero-inflation steady state, their steady state value is 0. (Except for i = r = 0.01)

Question 9

What is REE?

Answer 9

rational expectations equilibrium

It is a model-consistent equilibrium in the two-way relationship between the influence of expectations on the economy and the dependence of expectations on the time path of the economy.