5. Stetige Zufallsvariablen (fe/)

Question 1

was versteht man unter “stetigen Variablen”?

was folgt daraus?

Answer 1

= zwischen x_u und x_o unendlich viele / nicht abzählbare Werte liegen können.

Daraus folgt, dass man nicht mehr einzelne Werte beschreiben kann, sondern die Beschreibung nur noch für bestimmte Intervalle gemacht werden können.

• -> die Wahrscheinlichkeit für einen fixen Wert ist demnach:
• P* (X = x) = 0 für jedes x (also für einen einzelnen Wert)

Vermerk: x_u = untere Grenze und x_o = obere Grenze

Question 2

was beschreibt die Dichtefunktion / Wahrscheinlichkeitsdichtefunktion bzw. Dichte (_{= f(x)}) und wie lautet sie?

Answer 2

die Dichtefunktion beschreibt die Wahrscheinlichkeit für einen bestimmten Wertintervall (eines Flächenanteils unter der Kurve)

d = Kategorienbreite (von a bis b) geht gegen 0, womit es unendlich viele Kategorien gibt k → -∞

die Wahrscheinlichkeit für x_u ≤ X ≤ x_o ist genau das gleiche wie die Fläche zwischen dem Intervall [x_u; x_o]
–> wir können also die Wahrscheinlichekeit für das Intervall von ebd. beschreiben bzw. die Wahrscheinlichkeit für eine bestimmte Kategorie.

Question 3

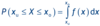
welche Normierungseigenschaft gilt bei stetigen Zufallsvariablen?

Answer 3

damit wir eine die Dichte als Wahrscheinlichkeit interpretieren können, beschreiben wir die gesamte Fläche unter der Kurve = 1.

das Intervall der Gesamtfläche reicht von -∞ bis +∞

*–> es ist also egal, ob das Intervall die x_u bzw. die x_o noch einschliesst oder gerade nicht nicht. (weil es egal ist ob es bis dorthin geht oder nur bis unendlich nahe daran)

Question 4

was beschreibt die Verteilungsfunktion?

Answer 4

Verteilungsfunktion = F(x)
mit ihr können wir die Wahrscheinlichkeit beschreiben, mit der eine Person HÖCHSTENS einen Wert von X aufweist (X ≤ x) –> also ist dies der Flächenanteil, der zwischen -∞ und x liegt. –> die Wahrscheinlichkeit hierfür = Wert der Verteilungsfunktion

Formal ausgedrückt: F(x) = P ( –∞ < X ≤ x) = P (X ≤ x)

Question 5

wie lautet die Formel für die Wahrscheinlichkeit, dass die Zufallsvariable X Werte im Intervall x_u ≤ X ≤ x_o ?
(Also P (x_u ≤ X ≤ x_o) )

Answer 5

F(x_o) – F(x_u)

–> wir rechnen also die Verteilungsfunktion von x_o minus die Verteilungsfunktion x_u

Question 6

wie lautet die Formel für die Wahrscheinlichkeit, dass die Zufallsvariable X Werte im Intervall –∞ < X ≤ x_o ?

(Also P ( –∞ < X ≤ x_o) )

Answer 6

= X ≤ x_o = F(x_o) – 0 = F(x_o)

–> die Wahrscheinlichkeit dafür, dass eine Person einen Wert erreicht, der grösser als –∞ ist und kleiner oder gleich wie die obere Grenze (x_o) ist also die Verteilungsfunktion von x_o (–> P ( –∞ < X ≤ x_o) ist ja genau das, was F(x) beschreibt)

Question 7

wie lautet die Formel für die Wahrscheinlichkeit, dass die Zufallsvariable X Werte im Intervall x_u ≤ X < +∞ ?

(Also P ( x_u ≤ X < +∞) )

Answer 7

= P ( X ≥ x_u) = 1 – F(x_u)

die Wahrscheinlichkeit dafür, dass eine Person einen Wert erreicht, der grösser oder gleich die untere Grenze (x_u) ist und kleiner als ∞ ist also 1 – F(x_u)

Question 8

was für Kennwerte gibt es für die stetige Wahrscheinlichkeitsverteilung? Nenne 5

Answer 8

1. Erwartungswert
2. Modus
3. p-Quantil x_p
4. Median
5. Varianz

Question 9

wie ist der Erwartungswert E einer stetigen Zufallsvariable X mit der Dichte f(x) definiert?

E (X) = ?

Answer 9

die Variableausprägung x wird it ihrer Dichte f(x) multipliziert und über die gesamte Fläche unter der Verteilung integriert.

Question 10

Was ist der / die … einer stetigen Zufallsvariable

1. Modus
2. Median
3. p-Quantil
4. die Varianz (Formel)

Answer 10

1. Modus = derjenige x-Wert, für den die Dichte f(x) ein Maximum besitzt
2. Median = der x-Wert, für den die Verteilungsfunktion F(x)=0.5 ist.
3. p-Quantil = analog zum Median → p-Quantil = der x-Wert, für den die Verteilungsfunktion F(x)=p
4. Varianz = die Streuung einer Wahrscheinlichkeitsverteilung

Question 11

Zeige an einer Verteilungsfunktion den Median und das 1. Quartil bzw. das 0.25-Quantil

Answer 11

zur Erinnerung: Verteilungsfunktion F(x) ist die kummulierte Wahrscheinlichkeit

Question 12

Was ist die Dichtefunktion für eine stetige Gleichverteilung? und was bedeutet “stetige Gleichverteilung”?

Answer 12

stetige Gleichverteilung = alle Werte dieser Verteilung sind gleich wahrscheinlich (quasi wie bei der Laplacewahrscheinlichkeit)
–> sofern sich x innerhalb des Intervalls [a,b] befindet

Question 13

mache ein Beispiel (Grafik) für eine stetige Gleichverteilung.

Answer 13

Question 14

wie lautet die Verteilungsfunktion innerhalb des Intervalls [a,b] bei einer stetigen Gleichverteilung?

Answer 14

Question 15

wie lautet der Erwartungswert einer stetigen Gleichverteilung?

Answer 15

Question 16

wie lautet die Formel für die Varianz bei einer stetigen Gleichverteilung?

Answer 16

Question 17

nenne Eigenschaften der Gauss-Verteilung

Answer 17

an den Rändern sehr niedrige Dichten und im Zentrum sehr hohe Dichten. Eine symmetrische Verteilung, bei der die meisten Werte nahe dem Mittelwert (µ) liegen. Gegen die Ränder sinken die Wahrscheinlichkeiten dann sehr stark.

Question 18

was ist der Erwartungswert und was ist die Varianz einer Normalverteilung (Gauss-Verteilung)?

Answer 18

• E* (X) = µ
• Var* (X) = σ² = (x_w – µ)² (Varianz bestimmt die Steile der Kurve)

µ = das Maximum bzw. der Modalwert

σ² entspricht den quadrierten Abweichungen der Wendepunkte vom Erwartungswert

x_w = Wendepunkt einer Verteilung → dort wo die Kurve ihr krümmungsverhalten ändert
→ x_w1 = links vom Maximum (µ); x_w2 = rechts vom Maximum (µ)
** also: Wendepunkte = µ ± σ**

Question 19

wie lautet die Formel für die Dichtefunktion einer Normalverteilung?

Answer 19

Pii = Kreiszahl Pii
exp. = Exponentialfunktion von...

Question 20

wie lautet die Formel für die Standardnormalverteilung (Z-Verteilung)?

Answer 20

ähnlich wie z-Transformation (wir können eine Verteilung der z-Werte beschreiben)

Question 21

wie lässt sich die Dichte der Standardnormalverteilung auch noch (einfacher) schreiben, wenn wir die Standardnormalverteilte Variable (=Z) kennen? (Formel)
–>

Φ (z) = ?

Answer 21

e = eulerische Zahl

Question 22

wie lautet die Formel für die Verteilungsfunktion einer Normalverteilung?

Answer 22

t repräsentiert die Werte von X, über die integriert wird (speziell für die Normalverteilung, ist so ne Konvention. aber Boris weiss auch nicht genau wieso…)

Question 23

angenommen wir wollen den Z-Wert für die Verteilungsfunktion (einer Standardnormalverteilung) von F(1.57) bestimmen, wie geht man da vor? (→ hier brauchst du die Tabelle A. 2)

was tun wir F(-1.57) bestimmen wollen?

Answer 23

Tabelle A.2

wir nehmen als erstes den Wert 1.5, “addieren” noch die 0.07 dazu. was wir bekommen dann die Verteilungsfunktion des Wertes F(1.57) als 0.9418.

also: 94.18% der Fläche der Standarnormalverteilung liegen links vom z-Wert 1.57.

F(-1.57) = die Fläche, die rechts vom Wert 1.57 liegt. (also der Rest von dem was links vom Wert liegt)
ganz einfach: die Kurve ist symmetrisch, also können wir rechnen 1 - F(+1.57) also: 1 - 0.9418 =0.0582
→ rechts von 1.57 liegt 5.82% der Fläche

→ damit kann man eigentlic jedes p-Quantil bestimmen (einfach auf der Tabelle A. 2 Kucken)

Question 24

wie berechnet man nun die Quantile einer Normalverteilung (ACHTUNG: NICHT die einer Standardnormalverteilung)
⇒ also für jede beliebige Normalverteilung

Answer 24

x_p = µ + σ · z_p

Wir können aus den Quantilen für die Standardnormalverteilung die Quantile für jede beliebige Normalverteilung berechnen.
⇒ wir machen quasi die z-Transformaion rückgängig
( zur Erinnerung: Z = X — µ) ÷ σ )

Beispiel dazu: welchem x-Wert entspricht das 95%-Quantil bei einer Normalverteilung mit den Werten µ=5 und σ²=100?

⇒ 5 + 10 · 1.645 (⇒den Z-Wert, den wir bei der Standardnormalverteilung haben )

auf den z-Wert kommst du mit der Tabelle A. 2 (da es keinen Wert für genau das 95%-Quantil hat, nimmst du einfach den Durchschnitt von den beiden, die am nächsten sind. hier wären das die z-Werte 1.64 und 1.65)

wir können das Ganze auch umdrehen indem wir sagen: uns interessiert, zwischen welchen beiden z-Werte (bspw.) die zentralen 95% der Verteilung liegt.
wir schreiben dann: P ( - 1.96 ≤ z ≤ 1.96)

Question 25

was sind zentrale Schwnkungsintervalle?

Answer 25

wie viel Prozent der Verteilung liegen zwischen einem bestimmten wert x_u und dem Wert x_o