5. Inter relationships between variables Flashcards
(19 cards)
Inter relationships between variables
the strength and nature of the relationship between two sets of figures
strength
correlation
nature
Is it a straight line? is regression used to try and find the equation
Correlation
2 variables are correlated if they are related to each other i.e. if the value of one changes does the other data set also change
can only ever be between +1 and -1
Scatter diagrams
data points are plotted on a graph x axis independent variable (we choose it) y axis is dependant on the value of x
regression
is what we use to work out the equation
Perfect positive linear correlation
r = + 1

Perfect negative linear correlation
r = - 1

High Positive Correlation
r ≈ 0.9
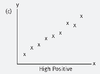
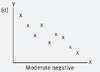
Moderate negative correlation
r ≈ -0.7
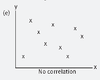
No correlation
r ≈ 0
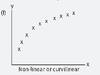
Non linear or curvilinear
N/A
Pearsons correlation coefficient
n = number of data points
FORMULA GIVEN IN EXAM

Coefficient of determination
take correlation coefficient and square it
makes it easier to interpret the coefficient of correlation
tells us the proportion of changes in y that can be explained by the changes in x, assuming a linear relationship.
i.e. correlation coefficient is 0.7, correlation of determination is 0.49, meaning 49% if the changes in y are caused by the changes in x and that 51% relate to other factors
Spurious correlation
where there is high value of correlation but no direct cause and effect
Regression
where the regression line has the equation y = a +bx
find b using formula
then use formula to work out a
a = mean of y - bmean of x

Interpolation
is when you estimate y when using a give value of x that is between the limits (outside the limit is extrapolation)
Limitations of linear regression
just because we have a straight line doesn’t mean it is useful for forecasting
need to assume the relationship many not be linear
it could be spurious
need to be careful when using the regression line for extropolation
Rank correlation: Spearman’s coefficient
when you want to calculate the correlation between two variables but one or both of them is not in a suitable quantitive form
i.e. student comes top in maths exam does that mean they will come top in econmics also, we interested in the rank not the absolute mark
d = difference in ranks
n = sample size



