4: testing materials Flashcards
properties of ceramics
hard - difficult to scratch brittle - easily shatter into pieces due to rigid structure stiff - difficult to stretch or bend due to strong bonds between atoms.
describe structure of a ceramic
the ceramics are either ionically or covalently bonded in a giant rigid
strong bonds between atoms make ceramics stiff.
however there is no pattern in its structure, the atoms are arranged randomly. this random atomic bonding means there are no slip planes in its ceramic lattice, as well as no mobile dislocations this makes ceramics very brittle.
being brittle is why cracks spread through them when they fracture, because the applied force acts over a very small area so the stress is high
PIC properties with desc of metals
some are malleable (can be shaped easily) and some are ductile (can be drawn into wires) this is due to the dislocations (missing atoms in metal structure) allowing planes (rows) of metal atoms to slip over each other when a force is applied
some are stiff - strong metallic bonds between ionic lattice and delocalised electrons
good conductors - metals have a sea of delocalised electrons that allows metals to conduct electricity
tough: it absorbs a lot of energy (deforms plastically) before fracture. this is because when you apply a stress the metal deforms plastically in the region of the crack, making the crack broader reducing stress around it
PIC structure of metals
crystalline metallic lattice - atoms are arranged in a regular repeating pattern
PIC what happens when you apply a force to a metal with dislocation
planes of metal atoms slip over each other
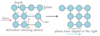
PIC what happens when you put the atoms of a second metal in dislocations what is this process called what’s the effect
atoms of a second metal (impurities) can be placed inside dislocations to pin them down, increasing the stress needed to cause slipping this is alloying this causes metals to be harder and less ductile
what is a perfect metal
a metal with no dislocations (missing atoms)
what is a polymer 2 types of polymers
a polymer is a molecular chain, made up of single repeating units called monomers there are man made polymers and natural polymers
example of polymer
rubber, sulfur atoms form cross link with polymer chains, the more sulfur = more cross links so more stiff polymer
PIC structure and bonding of a polymer
the monomers in a chain are covalently bonded so they’re very hard to separate polymer chains are often entangled but can be unravelled by rotating about their bonds when you pull them. this makes polymers flexible. the strength and number of bonds also affects the polymer’s flexibility. if the cross link bonds (chains tied at regular interval) are stronger and you have more of them, the more rigid the polymer
what is hooke’s law equation what is the constant a measure of,
for small extensions, the force F is proportional to the extension x F = kx F = force in newtons x = extensions in metres K = constant of proportionality (spring constant) Nm-1 the spring constant is a measure of stiffness, small when small force gives big extension, big when big force gives small extension
PIC what does the gradient of an extension force graph give you WARNING
the gradient for an extension force graph is the spring constant k k = f/x to get the gradient, sometimes it can get switched around by q’s so do 1 / gradient
PIC PRACTICAL: force extension graph for a rubber band explain the process
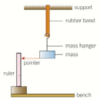
start with the shown apparatus, use a stiff wire wrapped around the bottom of the mass to provide a pointer measure the unstretched length of the band and then measure the length of the band with each mass you add on find the extension by subtracting old length from new length proceed to plot an extension against force graph
what is material compression what is the force called when you stretch a material
when you squash a material instead of stretch it if forces stretch the material they’re tensile
what is elastic deformation for a wire
when you deform a wire but it returns to its original length when force (stress) is removed
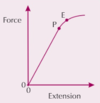
PIC what is the elastic limit E
the point up until an object elastically deforms
what is plastic deformation for a wire
a wire that has been permanently deformed and will not return to its original length when the stress (force) is removed
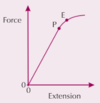
PIC what is the fracture stress B
the point after plastic deformation at which the wire breaks
PIC what is the limit of proportionality P
the point before the elastic limit where the graph is straight and extension is proportional to the force
what happens when you stretch a material
you store energy in it
2 equations to calculate energy stored in a spring
E = 1/2 Fx E = 1/2 Kx(x) = E = 1/2Kx²
what does the area under an extension force graph give when elastically deforming
when a body deforms elastically the energy stored is equal to the energy transferred stretching the spring the energy transferred stretching a material can be found from the area under the line
what is stress equation units
the force applied (tension) divided by cross sectional area (force per unit area) stress σ = tension / cross sectional area Nm-2
PIC what is the yield stress
the stress at which a material begins to deform plastically and become permanently deformed
what is strain equation units
its the change in length divided by the original length strain ε = extension / original length no units as it’s a ratio
what is stress dependent on what is strain dependent on
stress: cross sectional area strain: length
PIC what is ultimate tensile strength UTS
the max stress that a material can take before breaking
PIC stress strain graph for a brittle material
very little plastic deformation, graph is linear for all its length
PIC describe stress strain graph for mild steel
its a tough material and undergoes a lot of plastic deformation before fracture. this is why tough materials have rounded edges rather than sharp edges when under stress the steel may neck under the tension which is where part of it becomes narrower than the rest
what is young’s modulus equation units indication that ur value of YM is correct
YM is a measurement of stiffness stress / strain Nm-2 Pa YM is usually a large value
PRACTICAL: finding young’s modulus how to determine young’s modulus for a metal wire using Searle’s apparatus
basic: put wire under increasing tension and its extension is measured to find young’s modulus. the gradient of the linear stress strain graph will give you YM full: you must do a trial experiment then measure diameter and length of wire measure extension as more weights are added until the wire breaks, so you calculate breaking stress and strain calculate stress and strain from the data, plot on graph, linear section of graph will give you YM uncertainty can be estimated by choosing the largest source of uncertainty
PRACTICAL Explain, when testing Young’s modulus, why the wire should be as thin and as long as possible risk prevention procedures
The longer and thinner the wire, the more extends for the same force. This reduces the uncertainty in your measurements
safety goggles to be worn at all times due to risk of wire snapping and damaging eyes there will be a max load limit to not cross.
What happens to the relationship between force and extension after the elastic limit?
The material will stretch further for a given force
What is elastic strain energy?
The energy stored in a stretched material
Stress strain graphs for ductile materials…
Curve
Why is copper perfect for making electric wires?
Copper is ductile, and with its high electrical conductivity this means that it’s at the ideal for electric wires
On a stress strain graph for ductile material, what is the yield stress?
Here the material suddenly starts to stretch without any extra load.
When does the graph of force against extension start to curve?
When the force becomes great enough. Starts to curve after the limit of proportionality
Explain why the work done = Fx/2
Work done = force * displacement However, the force on the material isn’t constant. It rises from zero up to force F. To calculate the work done, use the average force between zero and F, F/2
Steel cables (on a crane) are strong, describe one other mechanical property that is important
stiff / high YM ; so does not stretch (too far under stress) / tough / not brittle ; so does not break easily / cracks don’t propagate / so does not snap easily
Why would plastic make a better plug casing than ceramics?
plastics are tougher, less brittle
define brittle
Undergoes little/no plastic deformation before fracture.
Describe the term tough
Toughness is a measure of the energy (impact) a material can absorb before it breaks.
what is strength
Describe strong materials
Strength is a measure of how much a material can resist being deformed (bent, stretched, fractured etc.) by a force without breaking.
Strong materials can withstand high stresses without deforming or breaking. This can be resisting a pulling force (tensile strength) or a squeezing force (compressive strength)
Describe the term stiff
describe a stiff material
Stiffness is measured by the Young’s modulus – the higher the value of the stiffer the material
Changing the shape of stiff materials is really difficult as they are resistant to both bending and stretching.
define ductile
Can be drawn into wires.
define hard
resists indentation on impact
define polycrystalline
to consist of a number of grains all oriented differently to one another, with a regular structure within each grain
