10: Modelling decay

Question 1

What makes nucleus unstable?

Answer 1

Too many neutrons, not enough neutrons, too many nucleons in total, or too much energy

Question 2

What happens to unstable nuclei?

Answer 2

They break down by releasing energy and/or particles, until they reach a stable form – this process is called radioactive decay

Question 3

Is radioactive decay a probability or random process? Why?

Answer 3

in radioactive decay a particle has a probability of decaying but this event is absolutely random you can’t tell when anyone nucleus will decay, or which nucleus in a sample will be the next to decay

Question 4

Describe how radioactive decay can be modelled

Answer 4

Based on a very large number of undecayed nuclei

Modelled by exponential decay

Question 5

define activity and units

Answer 5

the activity of a source is the number of nuclei decaying per second (easier to use activity)

measured in becquerels Bq 1Bq = 1 decay per second

Question 6

What is the activity of a sample proportional to? Why?

Answer 6

The size – as nuclei decay, the sample size gets smaller, so the activity falls

Question 7

what is half life

Answer 7

the time taken for the number of undecayed nuclei remaining to halve, or for the activity or count rate to halve

Question 8

how to find final activity having been given original activity and number of half lives done

Answer 8

final activity = original activity / 2^number of done half lives

Question 9

what is count rate

Answer 9

the number of particles emitted from the sample that the system detects per second

Question 10

Briefly describe the equipment used in the investigation of count rate

Answer 10

A Geiger counter attached to the Geiger-Müller tube which is on a clamp and stand. A protactinium generator in front of the tube.

Question 11

how will count rate differ from activity and what is their relationship

Answer 11

count rate will usually be smaller than the activity because not all emitted nuclei will be detected

however count rate is proportional to activity, if activity halves, count rate halves.

Question 12

What does the decay constant measure?

Answer 12

the fixed probability of a given nucleus decaying in a certain time interval. The bigger the value of the decay constant, the more likely a decay is, so the faster the rate of decay.

Question 13

how to find half life from a graphd

Answer 13

Find the value of undecayed nuclei when t=0 Go to half the original value of N Work out the corresponding time (You can check this by finding the quarter of N)

Question 14

how to find the undecayed nuclei N remaining after L half lives

Answer 14

N = 2^L number of undecayed nuclei remaining = 2^number of half lives

Question 15

equation to find activity

Answer 15

activity = λN

activity = fixed prob * nucleus decaying * number of undecayed nuclei

Question 16

how to determine the HL of protactinium

Answer 16

before you measure activity of source, measure background count sources to remove systematic error

use apparatus to record counts over 10 seconds for 3 minutes

find count rate by dividing counts in each period by 10 (to get count rate per second), now find correct count rate by subtracting this count rate from the background count rate

draw graph of count rate (y) against time (x) to find half life

Question 17

iterative equation for number of nuclei decaying in a time interval what does the negative sign show what type of equation is this

Answer 17

ΔN / Δt = -λN the negative sign shows the number of nuclei decreases after every decay

this is a differential equation

Question 18

what can we say about the relationship between the number of nuclei remaining and activity using the differential equation

Answer 18

the number of nuclei remaining is proportional to the activity ΔN / Δt ∝ -N

Question 19

what is a disadvantageous assumption made with iterative models for radioactive decay, and what is reality

how can you improve your iterative model

Answer 19

the line between each calculated value of nuclei remaining at a certain time is straight so the model assumes that the activity (and so number of nuclei) is constant during each time interval.

however really the rate of decay falls continuously as the number of undecayed nuclei remaining falls.

you can improve the model by reducing the time interval between calculations

Question 20

how to calculate half life if given decay constant

Answer 20

T1/2 = ln2 / decay constant

Question 21

what is the rearranged equation of the differential equation to find number of undecayed nuclei remaining and activity at a point

Answer 21

ΔN / Δt = -λN goes to

N = N0 e^-λt

N = number of radioactive nuclei

e = exponential constant

λ = decay constant

t = time (s)

A = A0 e^-λt

A = activity

e = exponential constant

λ = decay constant

t = time (s)

Question 22

graphical form of A = A0 e^-λt what does each part represent

Answer 22

lnA = -λt + lnA₀

y =mx + c

lnA = y

lnA0 = c

m = -λ (decay constant is positive, the gradient gives you negative decay constant)

x = t

Question 23

What is a capacitor? What is it made of?

Answer 23

Capacitors also store energy

Capacitors are made of two metal plates on which charge is built up and stored, separated by an air gap so that charge doesn’t flow between them.

electrons flow across the circuit from one plate to another, building up opposite charges

Question 24

Describe how capacitors store energy (using the circuit with battery, capacitor and bulb)

Answer 24

When the switch is flicked (so that the battery and capacitor are connected), charge builds up on the plates of the capacitor.

Energy provided by the battery is stored, in the capacitor, in the form of electrical potential energy

When the switch is flipped the other way, the energy stored on the plates fully discharge through the bulb, converting electrical potential energy into light and heat

Question 25

Describe what work is done on a capacitor charging

Answer 25

Work is done removing charge from one plate and depositing charge onto the other one. The energy for this must come from the energy stored in the battery

Question 26

Define capacitance

Answer 26

The amount of charge stored per volt

Question 27

capacitance equation units

Answer 27

C = Q / V capacitance C is in Farads, F which is C V^-1

Question 28

conversion of microfarads, nano-farads and picofarads to farads

Answer 28

microfarads = uF = 1*10^-6 farads

nanofarads = nF = 1*10^-9 farads

picofarads = pF = 1*10^-12 farads

Question 29

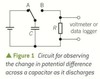
how do you investigate discharge of a capacitor

cap = 2200 uF

resistor = 10000 ohms

Answer 29

draw circuit as shown, you can use this to observe how pd across capacitor changes with time as it discharges

capacitor is charged at A

when at B it will begin discharging, as soon as this begins, start timing

for cap = 2200 uF and resistor = 10000 ohms, take readings every 5 seconds

for smaller values of either, take more frequent readings (could use data logger)

analyse data to draw graphs showing variation of charge, pd, current with time

Question 30

What does the graph of potential difference against charge look like? What is the area?

Answer 30

Straight line through the origin, area = energy

Question 31

Describe the graph of current/voltage/charge against time for a discharging capacitor.

Answer 31

All the same graph shape All start of high when t=0. All done exponentially decrease as time increases

Question 32

Describe the current of the discharging capacitor. Investigation of what happens when you charge/discharge a capacitor

Answer 32

The current flows in the opposite direction to the charging current. As the potential difference decreases, the current decreases as well

Question 33

Capacitor charging: Describe the graph of current against time

Answer 33

Current starts high when t=0 and exponentially decrease to 0 as time increases due to charge building up on the oppositely charged plates which increases electrostatic repulsion making it harder for more electrons to be deposited, and when pd across capacitor is finally equal to the pd across the battery supply, current is 0

Question 34

Capacitor charging: Describe the graph of voltage against time

Answer 34

Same as charge against time Voltage starts at zero, initially increases rapidly as time increases, then voltage increases slowly as time increases

Question 35

Capacitor charging: Describe the graph of charge against time

Answer 35

Same as voltage against time Charge starts at zero, initially increases rapidly as time increases, then charge increases slowly as time increases

Question 36

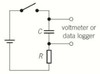
investigation for charging capacitor

Answer 36

make sure capacitor is fully discharged by connecting a lead across terminals of capacitor before charging

it will begin charging when switch is closed

record pd across it in equal time intervals, using data logger for short time intervals

Question 37

differential equation for rate of discharge

Answer 37

ΔQ / Δt = -Q / RC

resistance and capacitance are constant so rate of change of charge is proportional to the charge remaining

Question 38

diff equation to find charge, pd, current for discharging

diff equation to find charge, pd, current for charging

Answer 38

Question 39

What does the time it take to charge or discharge a capacitor depend on?

Answer 39

The capacitance of the capacitor. This affects the amount of charge that can be transferred for given potential difference

The resistance of the circuit. This affects the current in a circuit

Question 40

What is the time constant? Capacitors

Answer 40

The time taken for the charge, potential difference or current of a discharging capacitor to fall to 37% of its initial value

The time taken for the charge or potential difference of a charging capacitor to rise to 63% of its value when fully charged

Question 41

What is the relationship between the resistance in series with the capacitor and the time it takes a capacitor to charge or discharge?

Answer 41

The larger the resistance in series with the capacitor, the longer the capacitor takes to charge or discharge

Question 42

Why do you iterative methods only give you approximate answers?

What makes an iterative of method more accurate?

What is the disadvantage of using a smaller time interval, when doing iterative methods?

Answer 42

They assume that dx/dt doesn’t change over the time interval you’re using. In fact, dx/dt is changing all the time

Use a smaller value for the time interval

You need to do more iterations