Week 6 Flashcards
Homoscedasticity
Simply put, homoscedasticity means “having the same scatter.” For it to exist in a set of data, the points must be about the same distance from the line, as shown in the picture above. The opposite is heteroscedasticity (“different scatter”), where points are at widely varying distances from the regression line.
The volatility of the error term ?
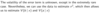
OLS variance
Difference between error term and residuals
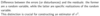
The variance of the OLS slope and intercept are defined as
The T distribution (also called Student’s T Distribution)
is a family of distributions that look almost identical to the normal distribution curve, only a bit shorter and fatter. The t distribution is used instead of the normal distribution when you have small samples (for more on this, see: t-score vs. z-score). The larger the sample size, the more the t distribution looks like the normal distribution.
If the normality of a and b holds, then the standardized OLS estimates are distributed as:
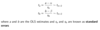
Hypothesis testing on OLS coefficients — we can test two different types of null hypothesis:
Hypothesis testing table:
Significance level
It should be clear from the discussion so far that whether we reject or do not reject the null hypothesis depends critically on α, the level of significance or the probability of committing a Type I error, the probability of rejecting the
true hypothesis.
Why is an alpha level of .05 commonly used?
Seeing as the alpha level is the probability of making a Type I error, it seems to make sense that we make this area as tiny as possible. For example, if we set the alpha level at 10% then there is large chance that we might incorrectly reject the null hypothesis, while an alpha level of 1% would make the area tiny. So why not use a tiny area instead of the standard 5%?
Type I error
Supporting the alternate hypothesis when the null hypothesis is true.
Type II error
Not supporting the alternate hypothesis when the alternate hypothesis is true.
Alpha Levels / Significance Levels: Type I and Type II errors example
In an example of a courtroom, let’s say that the null hypothesis is that a man is innocent and the alternate hypothesis is that he is guilty. if you convict an innocent man (Type I error), you support the alternate hypothesis (that he is guilty). A type II error would be letting a guilty man go free.
An alpha level is the probability of a type I error, or you reject the null hypothesis when it is true. A related term, beta, is the opposite; the probability of rejecting the alternate hypothesis when it is true.
Null hypothesis
Null hypothesis, H0: The world is flat.
Alternate hypothesis: The world is round.
Several scientists, including Copernicus, set out to disprove the null hypothesis. This eventually led to the rejection of the null and the acceptance of the alternate. Most people accepted it — the ones that didn’t created the Flat Earth Society!. What would have happened if Copernicus had not disproved the it and merely proved the alternate? No one would have listened to him. In order to change people’s thinking, he first had to prove that their thinking was wrong.
Solving the arbitraireness of choosing the alpha level
The p-value as a measure of evidence against Ho
Decision rule
Adjusted R-squared
