Week 4

Question 1

Answer 1

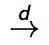
Stands for convergence in distribution

Question 2

Central Limit Theorem

Answer 2

establishes that, in most situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution (a bell curve) even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions.

For proof, c.f. the Galton Board

Question 3

Answer 3

Random sample sign

Question 4

Answer 4

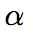
(the probability of false positive) is called size of a test

Question 5

Answer 5

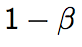
power of a test

Question 6

Type I Error

Answer 6

A Type I error (sometimes called a Type 1 error), is the incorrect rejection of a true null hypothesis. The alpha symbol, α, is usually used to denote a Type I error.

Question 7

Type II Error

Answer 7

A Type II error (sometimes called a Type 2 error) is the failure to reject a false null hypothesis. The probability of a type II error is denoted by the beta symbol β.

Question 8

Setting the alternative hypothesis

Answer 8

The choice of the alternative hypothesis depends on the problem under analysis.

Question 9

Defining the test statistic

Answer 9

Question 10

Computing the test statistic

Answer 10

Question 11

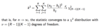
Critical value definition

Answer 11

A critical value is a line on a graph that splits the graph into sections. One or two of the sections is the “rejection region”; if your test value falls into that region, then you reject the null hypothesis.

Question 12

Answer 12

Question 13

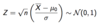
Confidence intervals

Answer 13

how much uncertainty there is with any particular statistic. Confidence intervals are often used with a margin of error. It tells you how confident you can be that the results from a poll or survey reflect what you would expect to find if it were possible to survey the entire population. Confidence intervals are intrinsically connected to confidence levels.

Question 14

Test statisitic formula

Answer 14

When you run a hypothesis test, you’ll use a distribution like a t-distribution or normal distribution. These have a known area, and enable to you to calculate a probability value (p-value) that will tell you if your results are due to chance, or if your results are die to your theory being correct. The larger the test statistic, the smaller the p-valueand the more likely you are to reject the null hypothesis.

Question 15

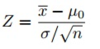
p-value

Answer 15

A p value is used in hypothesis testing to help you support or reject the null hypothesis. The p value is the evidence against a null hypothesis (the commonly accepted fact). The smaller the p-value, the strong the evidence that you should reject the null hypothesis.

Question 16

Two types of chi-square statistic tests

Answer 16

1. A chi-square goodness of fit test
2. A chi-square test for independence

Question 17

A chi-square goodness of fit test - what?

Answer 17

determines if a sample data matches a population.

Question 18

A chi-square test for independence - what?

Answer 18

compares two variables in a contingency table to see if they are related. In a more general sense, it tests to see whether distributions of categorical variables differ from each another.

Question 19

Chi-square test statistics

Answer 19

• A very small chi square test statistic means that your observed data fits your expected data extremely well. In other words, there is a relationship.
• A very large chi square test statistic means that the data does not fit very well. In other words, there isn’t a relationship.

Question 20

Error term

Answer 20

The error term includes everything that separates your model from actual reality. This means that it will reflect nonlinearities, unpredictable effects, measurement errors, and omitted variables.

Although the terms error and residual are often interchanged, there is an important formal difference. While an error term represents the way observed data differs from the actual population, a residual represents the way observed data differs from sample population data. This means that a residual is often much easier to quantify. Although an error is generally unobservable, a residual is observable.

The residual can be considered an estimate of the true error term.