Week 3.8 - LIF and Neurodynamics

Question 1

What is stochasticity?

Answer 1

The combined effect of multiple sources of perturbation that give a phenomenon the appearance of randomness.

Question 2

Where can you find stochasticity in the brain?

Answer 2

Stochasticity is present across all levels of brain activity. At the neuronal level, synaptic transmission is mediated by the stochastic release of neurotransmitters. Additionally, membrane potentials fluctuate due to the stochastic opening and closing of ion channels. Sensory input has stochastic components.

Question 3

What is the “recipe” for a Poisson signal?

Answer 3

(1) Determine a rate of random events
(2) Take an interval to spread them on
(3) Break the interval into small pieces
(4) take one interval at a time. If rand() < prob, fire.

Question 4

What is a synapse in an integrate and fire model?

Answer 4

An pre-synaptic event that induces a tiny post-synaptic voltage flick

Question 5

When are the neurons well-modeled by the Poisson process?

Answer 5

When:

• the average rate of the neuron is well defined (an homogeneous poisson process has a constant frequency).
• when the source of input to the neurons is unknown

Question 6

What is an advantage of leaky integrate and fire models?

Answer 6

They are good linear encoders, meaning the firing rate is proportional to the inputs.

They are especially adequate for modeling pyramidal cells.

Question 7

Name a few spiking phenomena that leaky integrate and fire models cannot reproduce?

Answer 7

They do not display

(1) No threshold adaptation
(2) No adaptive firing
(3) No resonant spiking
(4) No burst spiking
(5) No subthreshold oscillations
(6) No hyperpolarization spikes

Question 8

How many attractors are found in this 1D phase plane?

Answer 8

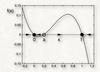
There are two attractors and one repellor.

The intersections with the horizontal axis are fixed points (dx/dt=0)

Question 9

Interpret this bifurcation diagram

Answer 9

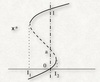
The horizontal axis is a parameter

The vertical axis indicates the locations of equilibria

For the range between I1 and I2 there are three coexisting equilibria, 2 stable, 1 unstable

Question 10

Interpret the fate of the trajectories for different initial conditions.

Answer 10

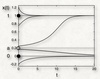
There are two stable states in this system, and trajectories in their range converge to them. There is also one unstable equilibrium, which repels trajectories.

Question 11

What happens with the equilibria as the parameter I is increased from I0 to I2?

Answer 11

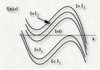
We see a stable attractor merging with an unstable attractor (i.e, a saddle node bifurcation).