Week 3

Question 1

Mean

1/ Sample mean
2/ Population mean

Answer 1

Suppose you live in a small street with 9 families. The annual income of these families is reported below (in 000) in the order the data was collected.

Question 2

Outliers

The mean is seriously affected by extreme values called ‘outliers’.

Answer 2

Example: As soon as a very high income earner into the
street, average income poorly represents the income of the household in the street.

Suppose: Income of the new family $200 (000)

Question 3

Median

Answer 3

Median

Question 4

Mode

The mode of a set of observations is the value that
occurs most frequently.

Answer 4

MODE: Newspaper readership

Mode = Most frequently read newspaper N2.

Question 5

Mode 2

Answer 5

Question 6

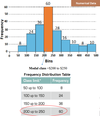
Mode 3 - Histogram

Answer 6

Histogram of the Neighbourhood income example

Question 7

Mean, Median, Mode
Which is the best?

Rule of Thumb (Numerical Data):

• Generally use the mean.
• But use the median for variables with skewed distributions and/or if there are outliers in the data (Recall median is not as sensitive to extreme values as is the mean).
• The mode is seldom the best measure of central location.

Answer 7

Ordinal/Nominal Data

• The calculation of the mean is not valid.
• Median is appropriate for ordinal data (which is ranked)
• For nominal data, a mode calculation is useful for determining highest frequency.

* Central location is not meaningful for nominal data as the data doesn’t have an order (categories can be put in any order which will shift the mode).

Question 8

Summary: Which measure to use?

Answer 8

1/ Compute the mean to: Describe the central location of a single set of numerical (or interval) data.

2/ Compute the median to: Describe the central location of a single set of numerical or ordinal (ranked) data.

3/ Compute the mode to: Describe a single set of nominal (or categorical) data but it is not a measure a central location in this case

Question 9

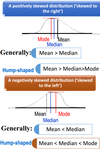
Relationship between Mean, Median and Mode

Answer 9

Question 10

Measures of Variability

Problem: Measures of central locations (Mean, median, mode). do not tell us anything the spread of the observation (distribution) around the mean.

i.e. how much are the observations spread out around the mean value?

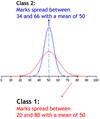
Mean =50

The mean of the two classes is the same (=50), but, class 1 has greate variability than class 2.

Answer 10

Solution: Measures of variability
• Range
• Variance
• Standard deviation

Question 11

The limit of Mean 2

Example: Consider two data sets (Same mean but different spread)

Answer 11

Question 12

Range

Answer 12

The range is the simplest measure of variability, calculated as:
Range = Largest observation – Smallest observation

Example:

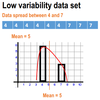
• Data: {4, 4, 4, 4, 4, 50} Range = 50 - 4= 46
• Data: {4, 8, 15, 24, 39, 50} Range = 50 – 4= 46

Question 13

Variance

Variance: Most important statistics used to measure variability.

Answer 13

Variance: the average of squared deviation of all observations from the mean.

Consider two small populations (N=5):

Both populations have the same mean, but the B is spread more around its means than A.

Question 14

Standard deviation:

Standard deviation: Play a vital role in almost all statistical inference procedures.

Answer 14

The standard deviation of a set of measurements is the square root of the variance of the measurements.

Question 15

When should we use Coefficient of Variation?

1

Answer 15

When should we use Coefficient of Variation?

2

Question 16

Interpreting Standard Deviation

Answer 16

Question 17

Empirical Rule

Answer 17

If a histogram is bell shaped, the rule says that:

1) Approximately 68% of all observations fall within one
standard deviation of the mean.

2) Approximately 95% of all observations fall within two
standard deviations of the mean.

3) Approximately 99.7% of all observations fall within three standard deviations of the mean.

Question 18

Example: Empirical rule (Risky investment)

A statistician wants to describe the way returns on investment are distributed.
- The mean return = 10%
- The standard deviation of the return = 3%
- The histogram is bell-shaped.
How can the statistician use the mean and the standard
deviation to describe the distribution?

Answer 18

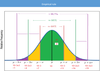
• Approximately 68% of the returns lie between 7% and 13% (within one standard deviation of the mean)
• Approximately 95% of the returns lie between 4% and 16%. (two)
• Approximately 99.7% of the returns lie between 1% and 19%. (three)

Question 19

Chebyshev’s theorem

Answer 19

Apply Chebyshev’s theorem when the distribution is not bell-shaped.

Chebyshev’s theorem:

For any data distribution, given that k is greater that 1, the proportion of observations that lie within standard deviations of the mean is at least 1–1/k².

e.g. k=2, 1–1/2²=0.75 or 75%,

k = 3, 1–1/3²=0.89 or 89%

Question 20

Chebyshev’s theorem

The average score on a math test: mean = 84

A standard deviation of 4 points.

Answer 20