Week 1.4 - Biophysical Neuronal Models and Neurodynamics

Question 1

What does this equation represent?

Answer 1

This is the Nernst equation. It describes the equilibrium potential of a single ion type. (e.g. Na+, K+)

Remember that the [square brackets] represent concentration and R, T, z and F are all constants

Question 2

What do we mean by stating that the cell membrane is

“Semi-permeable”

Answer 2

It means that not everything can pass or diffuse across the lipid membrane.

There are large molecules that cannot cross the membrane via ion channels, such as negatively charged proteins that contribute to the negativity of the resting potential.

Question 3

In a passive cellular membrane that is taken away from V_rest, what are the 2 constants that contribute to how fast V returns to V_rest?

Answer 3

Membrane capacitance (C_m)

& Leak Resistance (R_leak)

_{Their product is tau, the ‘membrane time constant’.}

dV/dt = (V-Vrest)/(Cm*R)

Question 4

What are leak channels?

Answer 4

Leak channels are passive ion channels. They are either always open, or they randomly (not as a function of voltage) open and close.

Question 5

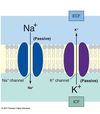
What is conductance? And how is it related to resistance?

Answer 5

Conductance (g) expresses how easy it is for the ions to flow through the cell membrane.

It is the reciprocal of resistance. That is,

g = 1/R

Question 6

How can we model the process of V tending to V_rest ?

Answer 6

With an ordinary differential equation

For the passive membrane;

dv/dt = -g_leak(V-V_rest)/C

Question 7

What is the driving force when a cell is at equilibrium?

Answer 7

0

( V = Vrest )

Question 8

What do gating variables represent?

Answer 8

The proportion of ion channels in a certain state (e.g., open/close).

So they take values between [0,1] .

Question 9

The conductance of an ion type is a function of …

Answer 9

Its maximum conductance and the state of the respective gating variables.

For example for Na+ we have;

Question 10

Why does capacitance (C_m ) affect the rate of change of membrane potential (V)?

Answer 10

Capacitance measures how well the membrane can store charge.

The better the cell can store charge, the slower the charge is releases.

Question 11

What is a model? List and discuss three desirable features of a model

Answer 11

A model is a representation for a phenomenon under study.

Accuracy, Predictive ability, Understandability. The desirable features are often in contradiction.

Question 12

What is a model? A good model?

Answer 12

A model is a representation. A good model is - representative, explanatory, consistent with other known models, predictive, quantifiable, simple, accurate. It encompasses phenomena qualitatively and gauges importance.

Question 13

What is a dynamical system? What is a state? What is a state variable? What is a phase space?

Answer 13

A dynamical system - a system whose state evolves over a state/phase space with time according to some fixed rule. What a system will do in the future is a function of where it is now.

A phase space (same as state space) is a set of all possible states (configurations) of a dynamical system.

A state of a system corresponds to a point in the state space.

A state variable is one of the variables that describe the current state of a dynamical system. State variables together fully define the state of the system.

Question 14

Regarding the differential equation plotted in this graph. From the left to the right, what are the types of equilibria we observe?

Answer 14

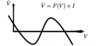
attractor, repellor, attractor

or

stable, unstable, stable

Question 15

Regarding the differential equation plotted in this graph. There are three intersections. What do we call them?

Answer 15

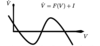
Fixed points.

Question 16

Regarding the following differential equation:

What happens with the equilibria if the F(V) is multiplied by 2?

What happens to the equilibria if we multiply F(V) by -1?

Answer 16

If F(V) is multiplied by 2, the equilibria will not change their stability. However, the particle will move faster through the phase space.

On the other hand, if F(V) is multiplied by -1, the stability of the equilibria will change. We will end up with two repellers and one attractor.

Question 17

What is the difference between a parameter and a state-variable?

Give examples of parameters and state variables of a Hodgkin-Huxley neuron model.

Answer 17

The state variable represents the current state of the model.

A parameter is constant over time (or changes slowly).

State variables of HH are: membrane voltage and gating variables of sodium (m, h), and potassium (n)

Some parameters of the HH model: Nernst potentials (E_Na, E_leak, E_K); capacitance, leak conductance, current input, maximum conductances.

Question 18

From the neurodynamics perspective, what causes a spike?

Answer 18

A spike appears due to the imbalance of two opposing processes.

1. Positive feedback through sodium conductance (m) which increases the membrane potential
2. Negative feedback through the inactivation of sodium channels and activation of potassium which reduces the membrane potential

Question 19

Consider a neuron model whose membrane potential is governed by the differential equation in the graph below.

Describe what happens with the membrane potential when we perform the following sequence of manipulations:

1. Clamp the voltage to the initial state V(0) and then release it.
2. Add a current step of I = 5pA to the neuron.
3. Next, we remove the added current.
   * What is the name of the phenomenon described above?*

Answer 19

1. Clamp the voltage to the initial state V(0) and then release it. → The rate of change for V(0) is negative, therefore the membrane potential would decrease and stop at the nearest attractor (equilibrium).
2. We add a current step of I = 5pA to the neuron. → When we add a current of 5pA, two equilibrium points are destroyed. We would only be left with one stable attractor. Therefore, if we initialized at V(0), the membrane potential would be attracted toward a higher membrane potential with variable speed.
3. We remove the added current. → If we remove the current step, the system regains two equilibria and we are left with two attractors and one repeller.

This type of change is a bifurcation. A bifurcation is a change such that when a parameter changes, the qualitative structure of the vector field changes dramatically (a fixed point is created or destroyed or changes its stability).

Question 20

How is a model like a neuron? How is it not like a neuron?

Answer 20

A model is a representation of a neuron. It can reproduce spikes that look like the action potentials measured in reality. But at the same time, it is not like a neuron, because it is not made of the same matter.

Question 21

In Neurodynamics:

A resting state of a neuron corresponds to…

A tonic spiking state of the neuron corresponds to…

Answer 21

…a stable equilibrium…

…a limit cycle attractor

Question 22

What is a trajectory?

What is a flow?

Answer 22

A trajectory is a sequence of states a system can occupy.

A flow is a set of possible trajectories of a system.

Question 23

What is a transient?

Answer 23

A trajectory before the system reaches a steady-state.

Question 24

When can we simplify a multidimensional model?

Answer 24

When (1) introducing details does not contribute to the goal of the model and (2) computational costs outweigh the benefits

Question 25

Name strategies to simplify a neuronal model

Answer 25

0. Reduce number of state variables
1. Remove Ion channels (gates)
2. Simplify Morphology (reduce number of compartments)

Question 26

What are some of the simplification strategies for a neuronal model?

Answer 26

1. Removing an activation variable - when its contribution is too little, when it is too slow, or when you simply want to explore the “what if” situation.
2. Making the activation instantaneous - when time constant tau is very fast.
3. Merging activation gates - when time constants are similar combine the two. For example, the tau of n and h are similar and can be combined into one function.

Question 27

Explain what kind of spiking behavior you see in the image:

Answer 27

Tonic firing - sustained response to a stimulus.

Also, ‘firing rate adaptation’, as the neuron fires more spikes at the onset of the stimulus.

Question 28

Explain what kind of spiking behavior you see in the image:

Answer 28

Phasic firing - transient response to a stimulus with spikes at the onset of the stimulus.

Question 29

Classify the following neuron as Type I or Type II and explain.

Answer 29

Type I Neuron: The Integrator

Frequency increases smoothly with increasing current.

Action potentials can be generated with arbitrarily low frequency (firing rate), depending on the strength of the applied current.

Question 30

Classify the following neuron as Type I or Type II and explain.

Answer 30

Type 2 neuron - The resonator

Firing frequency is relatively insensitive to changes in the strength of the applied current.

Question 31

What is the relevance of studying parameter spaces when studying spiking behavior?

Answer 31

By studying the parameter spaces, we understand the dependencies between spiking patterns and ion channel combinations.

The firing patterns of neurons are a consequence of the combinations of their parameters.

Question 32

How should one select state variables to include in a model?

Answer 32

One must attempt to obtain the most meaningful approximation of the natural phenomena under study.

For example, Hodgkin and Huxley selected V, because they could measure it, and m, n, and h variables because to produce an action potential ‘something’ had to be voltage-gated. And via pharmacological manipulations, they intuited that the action potential had to do with Sodium and Potassium ions.

Question 33

Given this F x I curve, is this neuron Type I or type II?

Answer 33

Type 1:

• arbitrarily low firing rates
• (mostly) linear increase of frequency with current

Question 34

What is plotted in the figure below?

Answer 34

An FxI curve

It measures the relationship between injected current and firing frequency of a given neuron.

Question 35

Given this F x I curve, what is the type of the neuron depicted?

Answer 35

A resonator,

A type 2 excitable neuron

• abrupt toggle between not firing and firing
• small modulation of frequency with current injected

Question 36

“Negative” current means that positive current goes _____ and that the neuron goes through _______.

Answer 36

inward/into the cell; depolarization

Question 37

The higher the capacitance, the _______ the potential difference comes to the resting potential.

Answer 37

the slower

Question 38

Why should neuroscientists learn nonlinear dynamical system theory?

Answer 38

Because neuron’s information-processing depends not only on the electrophysiological properties but also on their dynamical properties. Namely, the dynamics of bifurcation determine neuron’s excitability, spiking, its type, and so on.

Question 39

Define a bifurcation point/value.

Answer 39

The value of a parameter at which the quantitative structure of the vector field changes dramatically, a fixed point is created or destroyed or changes stability.

Question 40

How many parameters does the Izhikevich model have? How many dimensions?

Answer 40

Four parameters

Two dimensions (voltage and recovery variable)