week 1 SCM (chi-squared) Flashcards
why do we analyse frequencies when using at categorical variables?
- the numerical values you attach to different categories are arbitary
- this means that the mean of a categorical variable is meaningless
- because of this, we analyse frequencies of each category
what are the rows and columns of a contingency table?
- the columns are the conditions (i.v)
- the rows are the categories of the measure (d.v)
what is the general idea of the chi-squared test
it compares the frequencies you observe in certain categories to the frequencies that you might expect to get in those categories by chance
what is the chi-squared equation?
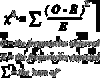
what is the equation for expected values, used in the chi squared eqution?
what is the degrees of freedom formula for chi squared tests?
(row total-1) *(column total-1)
What is the degrees of freedom for a contingency table with two columns?
1
this is because (r-1) * (c-1)
so
(2-1) * (2-1) = 1
what theory is the likelyhood ratio statistic based on?
The maximum likelyhood theory
this means that the probability for obtaining the observed set of data is maximised
this model is then compared to the probability of obtaining those data under the null hypothesis
therefore the resulting statistic is comparing the observed frequencies with those predicted by the maximised model
when would we use a likelyhood ratio statistic over a chi squared?
When the samples are small
what happens to the chi squared distribution as the degrees of freedom increases?
the peak of the curve moves to the right and the distribution spreads out
what does greater degrees of freedom mean in terms of how high the chi squared value has to be
the more degrees of freedom the higher the chi squared value has to be to be statistically significant
what is a problem with the chi squared test?
- the sampling distribution of the test statistic has an approximate chi squared distribution
- the larger the sample the better the approximation becomes
- however, in small samples the approximation is not good enough making the statistical significance test of the chi squared innacurate
what sample size is required for a chi squared?
- the expected frequencies in each cell must be greater than 5 for the chi squared significance test to be accurate
- what is the degrees of freedom of the likelyhood ratio?
the same as chi squared (rows-1)(columns-1)
what is a type 1 error and a type 2 error?
TYPE 1 ERROR= rejecting the null hypothesis when its actually true
TYPE 2 ERROR= failing to reject the null hypothesis when its actually false
what type of error does 2x2 contingency tables on the chi squared test tend to make?
type 1 error
this is because it tends to produce significance values that are too small
what is yates continuity correction?
- a correction to the chi squared formula to correct the fact that 2x2 contingency tables tend to make a type 1 error
- you subtract 0.5 from the numerator in the formula before you square it
- this lowers the value of the chi squared statistic and therefore makes it less significant
- some argues that this overcorrects and produces chi squared values that are too small
what are assumptions of the chi squared test?
- The chi squared test does NOT rely on assumptions that the data is continuous and normally distributed like other tests do
- data must be independent and contribute to only one cell of the table. this means you cannot use chi squared on repeated measures designs
- the expected frequencies of each cell should be no less than 5
what is a standardized residual?
a residual is the observed value - the predicted value
a standardised residual is a residual divided by its standard deviation
what two things can we used to break down the chi squared test statistic?
standardised residuals (z-scores)
or
effect sizes (
for larger contingency tables, what assumptions should we make for the chi squared test?
- no cell should have an expected frequency below 1
- up to 20% of expected frequencies can be below 5 but it will result in a loss of statistical power
- if you find yourself in this situation consider using fishers exact test
what is an odds ratio?
the ratio of the two categories
what is a significant standardized residual?
values outside of +/- 1.96
what technique would we use to analyse larger contingency tables with 3 or more variables?
log linear analysis
What is parametric statistics?
• Parametric statistics, such as r and t, rest on estimates of population parameters (x for μ and s for σ ) and require assumptions about population distributions (in most cases normality) for their probability calculations to be correct.
What are the two main uses of chi squared?
Goodness of fit (involving a single independent variables)
Test for independence (involving multiple independent variables)
LINK FOR HELPFUL WORKSHEET TO UNDERSTAND CHI SQUARED
https://www.cedu.niu.edu/~walker/statistics/Chi%20Square%202.pdf
What is the difference between residuals, standardised residuals and adjusted standardised residuals?
- The residual is O- E (observed - expected value)
- The standardised residual is O - E / square root of E. The mean of the standardised residual is 0 and the standard deviation is 1. If the standardised residual for a cell is beyond the range of +2 then that cell can be seen as a major contributer of the overall chi-square value
- The adjusted standardised residuals are standardised residuals that are adjusterd for the row and column totals
