Tutorial 4 - Frisch-Waugh Theorem, Omitted Variables, Instrumentral Variables Estimation Flashcards
Say we are interested in β₂: the effect of x on y, after controlling for w (=holding w constant).
How can we obtain the estimator ^β₂ according to Frisch-Waugh?
- Regress y on a constant and w. Take the residuals from this regression -> yres,w (the variation in y that cannot be explained by w)
- Regress x on a constant and w. Take the residuals from this regression -> xres,w (the variation in x that can not be explained by w)
- Regress yres,w on xres,w. The coefficient of xres,w is the same as the coefficient of x in the multivariate regression
This procedure illustrates the idea of filtering out the effect of w when estimating the effect of x on y.
Which conditions are met when the OLS estimator ^β is unbiased?
Unbiased: E(^β) = β
Note: If it is unbiased, that also means it is consistent:
What does this mean?
The OLS estimator is consistent:
How can you apply the Frisch Waugh theorem here?
- Regress log(invest) on a constant and trend and take residuals (“de-trended housing investment”)
- Regress log(price) on a constant and trend and take residuals (“de-trended house prices”)
- Regress the de-trended investment on de-trended prices.
Show that under the assumption of mean independence of the error term given the regressors, the OLS estimator is unbiased!
Show that the OLS estimator is consistent (under the assumption that the regressors and the error term are uncorrelated)!
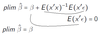
When is the OLS estimator unbiased?
if E(ϵ|X) = 0
i.e. if the error term and the regressors are mean independent.
When is the the OLS estimator consistent?
if Cov(x, ϵ) = 0,
i.e. if the error term and the regressors are uncorrelated.
How are unbiasedness and consistency related with each other?
Note that mean independence implies uncorrelatedness, but not vice versa.
Thus: if the OLS estimator is unbiased, it is also consistent. But if the OLS estimator is consistent, it need not be unbiased.
How do you call regressors that are correlated with the error term, Cov(x, ϵ) ≠ 0, i.e. where the OLS estimator will be inconsistent and biased?
the regressors x are endogenous
Why can regressors be endogenous?
- Omitted variables: x and y are both driven by a third, unobserved, variable
- Simultaneity: y causes x, rather than vice versa
- Measurement Error: x is measured with error
- Dynamic Models with Serially Correlated Errors
Which conditions does an instrumental variable z have to fulfill?
- Instrument relevance
- Instrument exogeneity
What is “instrument relevance”?
The instrument has to be correlated with the endogenous variable Cov(zₖ, xₖ ) ≠ 0.
In the present case with multiple covariates, a stronger condition is that in the regression below, the parameter 𝛿ₖ ≠ 0, i.e. the instrument zₖ has to be correlated with xₖ also when controlling for all exogenous covariates!
What is instrument exogeneity?
The instrument has to be uncorrelated with the error term. It has to affect the outcome only via the endogenous variable, i.e. it should not have a direct effect on the outcome:
How can you test relevance of the instrument with instrumental variables?
It can be tested by estimating the first stage regression (below) and use a usual t-test for H₀: 𝛿ₖ = 0. -> the more significant, the better.
For multiple instruments z₁, …, zₗ: use a test of joint significance of the instruments in the first stage. Rule of thumb: F-statistic >10 to have a “strong” instrument
How can you test exogeneity of the instrument with instrumental variables?
It is not testable, has to be justified based on economic theory.
What is a Two-Stage Least Squares (2SLS) Estimator? What is the first stage?
It is a way to carry out IV estimation:
- First Stage: Regress endogenous variable xₖ on all exogenous covariates 1, x₂, …, xₖ₋₁ and instrument zₖ, and form fitted values ^xₖ:
- ^xₖ contains only exogenous variation!
- It is important to include the exogenous covariates as well because the instrument has to affect the endogenous variable, conditional on the exogenous covariates
With a Two-Stage Least Squares (2SLS) Estimator: What is the second stage?
Second Stage: Regress the outcome variable y on all exogenous covariates and the fitted values^xₖ from the first stage -> coefficient on ^xₖ is the IV Estimator
What are practical issues with IV?
- Often standard errors for IV are much higher than for OLS (bias-variance tradeoff), in particular if there is a weak instrument problem, i.e. only a weak correlation between the instrument and the endogenous variable
- Always check the first stage regression!
- If the instrument is correlated with the error term, the IV estimator is not consistent. The inconsistency of the IV estimator might be even larger than for the OLS estimator…
Which test can you use to test for endogeneity of regressors?
Hausman test for endogeneity of regressors
What are the hypotheses with the Hausman test for endogeneity of regressors?
What is the idea of the Hausman test (null-hypothesis)?
Under the null hypothesis (xₖ is exogenous), the OLS and 2SLS estimators are both consistent, and should differ only by sampling error. A statistically significant difference between the two estimators would be seen as evidence against exogeneity of xₖ .
What is the test statistic and distribution for the Hausman test?
Under the H₀ of exogeneity, the Hausman statistic is asymptotically Xₖ² -distributed.
What are the limitations of the Hausman test?
- It assumes that the instrument is valid. Otherwise, a significant difference between OLS and IV could be driven by the fact that IV is inconsistent, which will not necessarily imply that xₖ is endogenous!
- Even in the case of a valid instrument, the test might have low power if the IV estimates are very imprecise (standard errors are high). In this case, the test might fail to reject the H₀ of exogeneity even if xₖ is endogenous.
What does the “Sargan test” test?
Overidenti cation test for validity of instruments
What can you do with an overidentified model?
overidentification test for validity of instruments
What are the hypotheses and idea behind the Sargan test?
Idea: under H0, the instruments should be uncorrelated with the 2SLS residuals.
What is the procedure of the Sargan test?
- Estimate the model using 2SLS and take residuals.
- Regress 2SLS residuals on all exogenous covariates plus instruments. Compute the test statistic, N * R²
- Under H0, the test statistic is asymptotically X² with q degrees of freedom (q= # instruments - # endogenous variables)
What could be problems with the Hausman test?
It is based on the assumption that at least one of the instruments is exogenous! (e.g., if all instruments are biased in the same direction, the test might not reject H0!)
What is a spurious correlation?
a statistical relationship between two variables appears to be causally related, but only appears so by coincidence or due to the role of a third, intermediary variable
