Topics 5 - Vector Calculus

Question 1

If you are reversing the order of integration, what do you need to remember about changing the limits?

Answer 1

You have to imagine how the limit equations overlap with respect to the new coordinate direction.

So a straight line going through the origin with a simple x² quadratic equation coming from beneath (i.e. the straight line is the upper limit and the quadratic lower limit) becomes a straight line for the lower limit and a √(y) for the upper limit.

You can visualize the shape. With respect to the y-axis x² is √(y).

Question 2

What do you need to remember about this question?

Answer 2

You need to read the question carefully. They say the cylinder is resting on x-y plane, thus the portion on the x-y plane is equivalent to the area of a circle.

Question 3

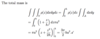
What would the values of the limits be if you reverse the order of integration?

Answer 3

The upper limit x = cos^-1(y) converts to y = cos(x).

Question 4

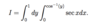
Why is the order of integration reversed sometimes?

How is it done?

Answer 4

Reversing the order of integration can make the integral easier to evaluate.

The inner integral defines the shape of the region over which integration is to be done.

You cannot just write the same limits in the opposite order.

The inner integral should have the variable limits and the outer integral should have constant limits.

It is a good idea to sketch the shape and determine the new limits of the shape.

Question 5

What is the best way of determining what the limits are when you change the order of integration?

Answer 5

Determine the sketch of the limits. Including all the constant values.

Then flip the axis so that y becomes horizontal and x vertical. From there determine the necessary limits to achieve the same results.

Question 6

What’s an important thing to remember about doing double integrals compared to single integrals?

Answer 6

You need to make sure you understand the limits. The limits are key in double integrals.